|
Цельность и организация 3 – это три элемента и три измерения мира и наших мыслеобразов, самая жесткая фигура. 7 - это число простых сочетаний из 3 элементов, 12 - это число сочетаний с учетом доминанты, 15 - это полное число сочетаний из 3 элементов. Плюс у материального тела есть вес, температура и подвижность (пульсация, вращение...). И с точки зрения просто объема следует учесть основные пространственные структуры: тетраэдр, куб, октаэдр, додекаэдр.
Например если сжать ком шариков из пластилина, то в центре получим фигуры оптимальной упаковки - это квазидодекаэдры, вероятностно тяготеющие к фигуре ограниченной 13 гранями, 10 из которых пятиугольники. Добавим пульсацию давления и получим здесь энергетический квазиикосаэдр (число граней 21). Подобный процесс происходит внутри пены, внутри вещества, я ядрах светил и сложных атомов. Это источник золотой пропорции - пропорции Вселенной - основы природной цельности, организации и творчества.
Все пульсирует, вибрирует, вращается, течет и изменяется.
Выводы. 1. Золотое сечение формируется уже на уровне атомных ядер, благодаря плотной упаковке. 2. Это не точно "золотое сечение" - это тяготение к золотому сечению, квази-золотое сечение. При этом оно объемно, нелинейно пульсирует и колеблется, вращается и структурно "выворачивается". То есть динамично. 3. Все платоновы тела и другие эффективные многогранники представлены в структуре общего излучения-влияния Земли. Вложены-соединены-переплетены друг с другом подобно волнам. 4. Возможно в центре Звезд и Планет находится суператомное ядро-частица, окруженное слоями супер-частиц поменьше. Общая масса этого сверхядра может составлять миллионы и миллиарды тонн и более (в звездах). Вокруг этого ядра и происходят колебания-вращения Коровякова (см. ниже). Структура пены и плотной упаковки (додекаэдры)Задача об упаковке - лучшее решение + здесь Пенометаллы и пенокерамика - материалы будущего Пены - это и мыльные пузырьки и полистирол и пенобетон и керамические пены и металлические... Монодисперсные пены (пузырьки одинакового размера) тяготеют к додекаэдрной форме внутренних пузырьков. Аналогичную структуру принимают и клетки растений/деревьев и клетки животных организмов. А также упругие одинаковые шары под давлением (например, атомы простых веществ или нуклоны больших атомных ядер). "Земляника растет и под крапивой",- подметил
Шекспир. Геометрическая мысль плодоносит и в худших условиях. "Я
сдавливал свежий горох в одном и том же котле с силой в 1600, 800 и
400 фунтов,- писал еще в 1727 году Стефан Хейлс в своей "Статистике
растений",- при этих опытах горох расплющивался, но его уровень не
повышался, так как под действием большого веса масса гороха
заполняла промежутки между горошинами, которые превращались в
прелестные маленькие додекаэдры". Через двести с лишним лет, в 1939
году, опыт этот повторили два ботаника - Д. Марвин и Э. Мацке. Они
заменили горошины свинцовыми пулями и увеличили давление в десять
раз. Получились неправильные четырнадцатигранные тела. Грани были по
преимуществу пятиугольными, хотя среди них встречались и четырех- и
шестиугольные. Далее было обнаружено, что внутренние клетки
растительных тканей тоже имеют в среднем четырнадцать граней.
Исследовали под микроскопом пену, состоящую из двух тысяч пузырьков.
Те шестьсот из них, что расположились в центре, имели в среднем по
13,7 касания с соседями, но чаще всего они превращались в
тринадцатигранник, составленный из одного четырехугольника, двух
шестиугольников и десяти пятиугольников. В 1959 году Джон Бернал
изящнейшим образом показал, что пятиугольная грань действительно
имеет преимущество перед другими. Он изготовил из пластилина массу
одинаковых шариков, вывалял их в меловой пудре, а затем спрессовал в
сплошной ком. У получившихся фигур в среднем было 13,3 грани, в
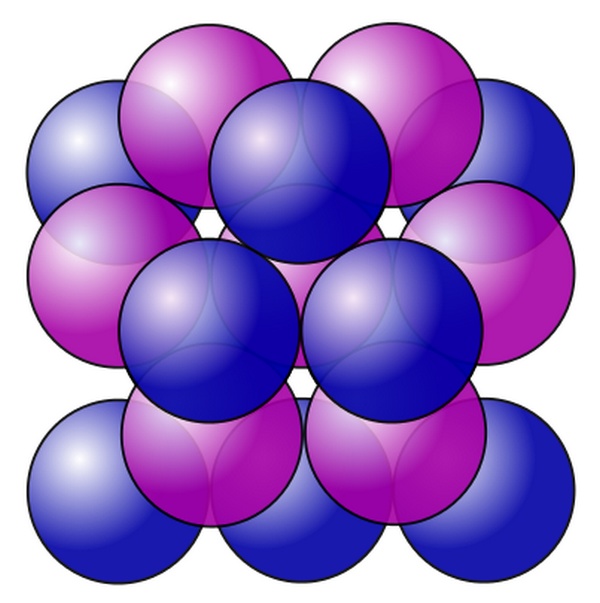
большинстве своем пятиугольных. Получается, что надуваем мы материю или сдавливаем - в итоге имеем додекаэдры. Это оптимум микроструктуры, пронизанный золотыми сечениями. В общей картине мы приходим к ряду платоновых тел - тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. При этом добавляя к материальной структуре энергетическую (пульсация по центрам граней, надувание/сжимание), получаем взаимные пары: тетра-тетра, кубо-окта, доде-икоса. Первые две пары образуют базовые молекулярные структуры благодаря своей пространственной экономичности (плотная упаковка, то есть то же сдавливание с учетом отталкивания протонов). Отметим здесь, что гексагональная структура - это плоскостное распределение, а мы ведем речь о объеме. То есть гексагональные структуры проявляется обычно в плоскости (снежинки) или на поверхности (пчелиные соты). Переход от тетраэдрам к кубам и от кубов к додекаэдрам существует явно геометрически. Это вписание фигур через диагонали. Смотрим картинки.
Подобный переход мы видим и в структуре плотной упаковки шаров. На рисунке ниже внешняя форма соответствует кубу, а внутренняя октаэдру. При этом углы упаковки выложены тетраэдрами. А если вовнутрь засунуть центральный шар, то получим гексагональную плотнейшую упаковку, где внутренний шар соприкасается с 12 внешними. Если шары мягкие и их равномерно сдавить, получим ромбододекаэдр. Фигура удивительная, ведь ею можно замостить пространство без щелей. Но мы уже знаем, что природа сдавливает несколько иначе и шары адаптируются друг к другу и - в объеме - плоскости и перпендикуляры ломаются и получаются квазидодекадры. Хотя все вроде логично: 12 граней - это и есть додекаэдр.
При надувании или сдавливании додекаэдра силовые-энергетические сопротивления минимальны по центрам граней, проявляя силовой икосаэдр устойчивости додекаэдра как целостности. На картинке можно видеть, что эти силовые линии можно сгруппировать в треугольники (икосаэдры), четырехугольники, ромбы (двойные треугольники), пятиугольники - основные и большие. Так вот, эффект Коровякова говорит любителям додекаэдрно-икосаэдрной модели Земли, что эта структура подвижна энергетически относительно поверхности Земли (делает оборот за сутки). Еще один шутливый нюанс. Домики в стакане порождаются все-таки неким объемным додекаэдром ядра, поэтому возможны домики вертикальные - например в масштабе человеческого жилища. Вся сила в чердаке )
|
Тетраэдр - Куб - Додекаэдр
Такие фигуры - тетраэдр, куб, додекаэдр - образуют шарики, если их
сдавливать. Конечно, знание азбуки мешает воспринимать поэзию природы и вольной логики. Поэтому неграмотному или двоечнику легче даются дедуктивные построения. Об этом еще Гегель писал в статье "Кто мыслит абстрактно?" и – следовательно – неуч легче и проще все обобщает. Самое универсальное возражение здесь: Кабы было все так просто... И Шерлок Холмс подсказывает нам, что дедукция хороша только при исключительном внимании к деталям. Можно ответить теоремой Ласло Тота, который доказал что на плоскости самая плотная упаковка кругов шестиугольная. Квадратная - похуже, но тоже рулит. Поэтому переходя в объем получаем тетраэдры.
– А вот фиг! Складываем пушечные ядра и получаются пирамиды =
полуоктаэдры. Или не фиг? А если все-таки сложить тетраэдрами?
Встречаются конечно и упертые технари-троечники, которые не овладев
высшей химией мат.анализа - на котором написаны ВУЗовские учебники
по физике - пытаются все перепроверять наглядным способом,
единственно доступным конкретному естественному разуму. И они могут
обнаружить и воскликнуть АГА! - Молекулы то в тетраэдры не складываются! Это же
молекулы! И приводят свои доводы. Например, такие...
Ну да. В тетраэдрах атомы группируются-кооперируются и их связи
связываются. Поэтому эти микро-семьи несколько дистанируются друг от
друга и получаются пустоты и кубическая решетка оказывается плотнее.
Хотя....
В общем ну его... Еще Платон сказал что Земля сверху выглядит как
додекаэдр. Поэтому пусть так оно и будет. Ведь не случайно автор
додекаэдро-искосаэдрной Земли Гончаров был художником и начинал с
пирамид и рисунков Наска... Тема благодатная... Правда не все видят одинаково эту самую георешетку.
Янтры индийские - очевидно глядят в ту же сторону. А из космоса плохо видно. Наверное далеко потому что.
А вот картинка, одобренная издательством "Наука" в непростом 1990 году (это я к тому что статьи о ИДСЗ любят начинать с фразы: вот дескать ученые обнаружили, хотя это всего лишь гипотеза - к тому же неакадемическая).
Внутри книжки много разных картинок. Но любителям тетраэдров и додекаэдров там пищи нет. То что решетки разные - это дело простое. Как волны вкладываются и накладываются друг с другом, так же складываются и решетки.
Дедукция - метод верный и сильный. Но он хорош в сочетании с
индукцией, т.е. со знанием деталей и учетом всех точек зрения. То
есть хорош в рамках Общего метода Декарта. И мы только что учли несколько весомых точек зрения. И поэтому можем сделать новый шаг: в самую глубину обобщений и дедукции |
|
Заглянем в вглубь атомного ядра. Как если бы смогли. И там мы увидим сплюснутые шарики-нуклоны. И если подумать/представить, то тетраэдры и кубики получаются сами собой. Плюс добавим энергетические связи-вибрации-пульсации между шариками и обнаружим пары: • тетраэдр-тетраэдр (вывернутые из центров граней друг друга) • куб-октаэдр (то же самое, куб пульсирует и энергия в нем тоже пульсирует - через грани и их центры, дополняя кубическую материю октаэдрной энергией) И тут вдруг снизойдет на нас озарение о пяти платоновых телах и мы узрим еще одну пару = додекаэдр-икосаэдр!!!
Правда эта парочка не совсем правильная. Там
квазидодекаэдр-квазиикосаэдр. И поэтому в природе рулит (из самых
глубин материи) квазизолотое сечение. Читаем еще раз. Икосаэдров там не получалось. Но энергетически они есть! А теперь обобщаем до Земли. В ее глубине атомы сдавлены и в самом центре ядра ведут себя подобно шарикам....
Здесь секрет 6-конечной и 8-конечной и 12-конечной звезд. Ну и так как Солнце - это наше все... то помедитируем и на него.
Дополнительные точки зрения. ПС1. И хотя в глубинах материи мы видим теперь квази-додекаэдры, все же физический мир подчиняется гравитации и простоте. Поэтому кубическая архитектура остается самой востребованной в разумном строительстве. Попробуйте строить здание додекаэдрами или шарами и вы сразу это поймете. Плюс теперь у нас есть более чистый и глубокий взгляд на природу Каабы и египетских пирамид. Мы же все понимали, что там дело в энергетике - раз уж речь о Боге. А теперь и знаем.
ПС2. Теперь и модель ИДСЗ представляется не вполне корректной.
Точных углов на поверхности не получается по квазипричине. К тому же
такой механизм действует на уровне ядра Земли и это ядро, похоже,
движется несколько иначе чем земная кора. К этому выводу нас
подталкивают элементарная логика жидкой мантии и странные опыты
Коровякова.
Эксперимент Коровякова с движением пятиугольника показывает, что есть прямое влияние земного ядра и, очевидно, что это влияние и само ядро подвижны. О Коровякове и его опытах (сборка) смотрите ниже. ПС3. Впрочем в процессах энергетика земного ядра должна проявляться. В каждом конкретном случае по своему. Добавьте сюда сезонное смещение Солнца относительно Мировой оси, его собственное вращение, а также движение Луны и планет... Не забыв о конкретном месте процесса - географическом и геологическом. Учет этих факторов требует понимания вселенской природы гравитации (микро-микроизлучения всех звезд + эффект их экранирования большими массами + эффект гравитационного накопления материи в ядрах звезд и планет + модель атомного ядра как 'точка сборки' Вселенной).
|
|
Николай Иванович Коровяков
(1937-2004), с 1959 по 1989 год начальник конструкторского бюро
охотничих ружей Тульского оружейного завода. Разработчик
ружья "ТОЗ-34"
и его модификаций. Дважды удостоен высшей премии оружейников -
премии имени С.И. Мосина. Открыл эффект Коровякова (пятиугольная
структура собирания частиц при остановке вихря в жидкости,
парадокс чаинок) и разработал на его основе динамическую модель
ядра Земли.
 Действительный член Российской Академии Естественных
наук, почетный член Академии Космонавтики им. К.Э. Циолковского.
Статья в Википедии. Действительный член Российской Академии Естественных
наук, почетный член Академии Космонавтики им. К.Э. Циолковского.
Статья в Википедии.
Существо эффекта Коровякова (здесь можно выделить статью Чернуха В.В. «Чаиночный парадокс»): • Раскрученные чаинки собираются в итоге в центре стакана в
пятиугольник, который при повторении опытов медленно вращается и
делает полный оборот в течение суток. Это говорит либо о
зависимости пятиугольника от вращения Земли, либо о зависимости
от направления на Солнце, либо о зависимости ориентации от звезд
(как у гироскопа). Артур Васильев Фотографии из статьи "Чаиночный парадокс"
|
|
Здесь собраны статьи о открытии Коровяковым сил неизвестной физической природы. Гидродинамический волчок Коровякова Чернуха В.В. «Чаиночный парадокс» (основная статья) Структура пены и материи (додекаэдры) (основное объяснение) Геофизический стенд Коровякова М. Рац. От стакана с чаем до Бермудского треугольника («Наука и жизнь», №5, 1987) Украинцев Борис. / Тайная симметрия (Журнал «Природа и человек», 1990, № 8) АЛЕУТСКИЙ. Пятиугольный мир Коровякова С.Кашницкий. Катастрофа в вихре тайн (На грани невозможного 10, 2006) |
|
Гидродинамический волчок Коровякова Гидродинамический волчок, содержащий полый корпус, который выполнен из прозрачного материала и заполнен прозрачной жидкостью с включениями в виде различных по массе и цвету частиц, и неподвижное основание, связанное с корпусом, согласно полезной модели, снабжен втулкой для связи неподвижного основания с корпусом, верхняя часть которой закреплена в днище корпуса, а ее нижняя торцевая поверхность размещена относительно неподвижного основания с зазором, и соосно установленным во втулке застопоренным стержнем с заостренным верхним концом, упирающимся в тело втулки, и нижним концом, закрепленным в неподвижном основании.
|
Украинцев Борис"Тайная симметрия".
Журнал «Природа и человек», 1990, № 8, стр. 28-31.
Предсказание землетрясений и... авиакатастроф,
прогнозирование направления дрейфа материков и океанических
течений, указания на местонахождение алмазных трубок и нефти,
исчисление дней биологической активности и зловещей активности
«Бермудского треугольника» и других подобных ему «черных дыр»
Земли. Наконец, возможно и создание безынерционных летательных
аппаратов (по типу НЛО) и управление гравитацией и течением
времени... Сама постановка в один ряд столь несовместимых и
подозрительно экзотических явлений и феноменов способна вызвать
проницательную усмешку. В самом деле, какая тут связь? Её нашел
тульский оружейный конструктор Николай Иванович Коровяков.Мало же было Коровякову смущать высокие академические лбы парадоксами своего гидродинамического волчка, так он ещё начертал на его овалах и плоскостях мрачноватые назидания. Например, такое: «Классификация элементарных сущностей в современной физике подобна неблагодарному труду ассенизатора, однако это единственный и реальный путь прорыва к познанию многоликой природы через ширму научных школ и господствующих авторитетов». И подпись: «Конструктор Тульского оружейного завода, изобретатель СССР, Н.И. Коровяков, 1985».
|
|
«Чаиночный парадокс»В.В.Чернуха ......... Прекрасная статья. Представлено полновесное исследование эффекта Коровякова с возможностью повторить такие опыты самостоятельно. С другой стороны, есть более простое объяснение эффекта Коровякова структурой плотной упаковки (смотрите здесь и здесь). Это объясняет и формы пятен и статистику опытов. Поэтому абстрактная кварковая поляризация от автора исключена из текста. Если есть желание познакомиться с ней - здесь полный текст статьи.
2. Загадки вращения чаинок. С загадочными свойствами вращения мы встречаемся и на бытовом уровне, но, как правило, не обращаем на них должного внимания. Классическим примером считается поведение чаинок при размешивании сахара в стакане чая. Покружившись, они, в конце концов, укладываются курганчиком на дне в окрестности его центра (подобный эффект имеет место и в локальном атмосферном вихре, где частички концентрируются вблизи его оси). Мы привыкли к тому, что более плотные частицы (а намокшие чаинки плотнее воды и тонут) при вращении отбрасываются к стенкам сосуда. Этот центробежный эффект используется в центрифуге. Но в стакане чая всё происходит наоборот, т.е. существует некая сила, преодолевающая действие центробежной силы. О ее природе долгое время шли споры. Эффект проявляется при остановке вращения, поэтому сравнение с центрифугой неадекватно. И. Ньютон считал, что центробежных сил в потоке вообще нет. Э.Мах
и Некоторые полагали причиной циркуляции образование воронки во вращающейся жидкости. Сегодня считается, что классическая гидродинамика в состоянии объяснить этот феномен, т.е. «чаиночный парадокс» разрешен. Однако не все с этим согласны. Один из оппонентов – Н.И.Коровяков – в конце прошлого века открыл новый феномен, классической гидродинамике неподвластный. Началось с того, что он усомнился в эффекте воронки и поставил опыт с вращением закупоренного и заполненного водой цилиндра, где образование воронки невозможно. Устройство было выполнено в виде волчка. Вместо чаинок использовалась разноцветная пластмассовая крошка. Вращающиеся частички устремлялись к оси, причем более массивные это делали быстрее [2]. Однако это был не главный результат опытов Коровякова. Он обнаружил, что пластмассовая крошка застывает на дне в виде правильного пятиугольника с немного размытыми вершинами. Это было неожиданным и противоречащим гидромеханическим представлениям. Неожиданным оказалось и «поведение» пятиугольника. Его вершины от опыта к опыту смещались в направлении, противоположном вращению Земли, и ровно через сутки занимали исходное положение. В зависимости от времени суток и времени года пятиугольник выглядел то четко, то весьма размыто. При полной Луне его очертания были особо строгими. Н. Коровяков объяснял открытое им явление свойствами ядра Земли, внутри которого он предполагал существование пентасимметрии [2]. К сожалению, в научной литературе результаты Коровякова опубликованы не были и квалифицированного обсуждения, подтверждения или опровержения не получили. Тем не менее, опыты Коровякова возродили «чаиночный парадокс», обогатив его новым содержанием, выходящим за рамки классической гидродинамики и указывающими на возможность поляризационных процессов с образованием пяти t-зарядов на частичках, благодаря которым они дистанционно взаимодействуют друг с другом. Подобное коллективное взаимодействие в классической гидродинамике отсутствует и требует иного подхода для анализа феномена. Коллективный эффект усложняет анализ. Поэтому целесообразно изучение нового феномена начать с изучения затухания вращения одиночных частиц, что дает нам представление о динамике системы невзаимодействующих частиц и позволит в дальнейшем оценить роль коллективных эффектов. Поскольку перемещение частичек к оси происходит при их опускании
на дно, то можно предположить, что наличие свободной поверхности и
постепенно исчезающей воронки не должно влиять на формирование
центрального пятна осадка. Тогда появление правильных пятиугольников
возможно и в стакане чая. Однако, несмотря на распространенность
чаепития, об обнаружении пентасимметрии, насколько нам известно, не
сообщалось. Чтобы разобраться в этой противоречивой ситуации и
понять, действительно ли возможна пентасимметрия осадка,
необъяснимая в рамках классической гидродинамики, была осуществлена
серия опытов в постановке, доступной любому желающему их проверить.
Опыты проводились в сентябре 2006г. в дневное время. 3. Движение одиночных частичек во вращающейся жидкости. Естественно считать, что для одиночной частицы поляризационные эффекты отсутствуют. Поэтому ее смещение к оси должно описываться классической гидродинамикой. Действующая на частицу центростремительная сила обусловлена радиальным градиентом давления во вращающейся жидкости. Если пренебречь трением частицы о дно (и иными силами, меняющими ее угловой момент и энергию), то вращающаяся частица должна совершать радиальные колебания, поскольку с удалением от оси центробежная сила убывает, а центростремительная растет. Поэтому центробежное ускорение сменяется центростремительным, и, наоборот, при приближении к оси преобладающей становится центробежная сила. При учете трения, снижающего энергию частицы и ее угловой момент, ее колебания затухают, а центр колебаний смещается к оси и через несколько оборотов частица фиксируется в центре дна, где вращение жидкости отсутствует. При наличии трения о дно скорость частицы в равновесном состоянии равна нулю. Поэтому ее смещение к оси и остановка там – это переход к равновесному состоянию, не совместимому с продолжающей вращаться жидкости. Опытные данные позволяют выявить величину и природу силы трения частицы о дно, проявляющуюся в зависимости силы трения от массы частицы и скорости вращения. Опыты с одиночными частицами проводились в цилиндрической чашке диаметром 9,5 см и уровнем воды 3,5 см. Они раскручивались ложкой (или лопаткой), движущейся с частотой около 2 Гц. Сравнивалось поведение частиц трех видов: Массы этих частиц находятся в диапазоне ~10-3 – 1 г. Первые два типа частиц (А и В) всегда останавливались в центре дна. Частица А1 достигает оси за ~7 с, частицы А2, А3 и В – за 10-12 с, частица А4 – за 10-15 с. Остановка частиц происходит при вращающейся жидкости. Процесс релаксации занимает ~ 10 оборотов. Основную часть времени частицы вращаются без смещения к оси в режиме радиальных колебаний. Заключительное движение к оси происходит за время, грубая оценка которого дает 1–2 с (1–2 оборота) и не зависит от массивности и типа частиц. Частица С имела два вида траекторий: один приводил ее в центр дна за 10–15 с, где она фиксировалась, тогда как другой, существенно более редкий, длительностью 25–30 с подводил ее к оси, а затем уводил из центра к стенке чашки, где она останавливалась. Из этих опытов следует, что время остановки частиц возрастает в 1,5–2 раза при увеличении массы на три порядка. Это означает, что сила трения, отнесенная к единице массы, практически постоянна. Отсутствие зависимости от массы характерно для силы «сухого» трения fмп = k mg, где g обозначает ускорение свободного падения, а k - коэффициент трения. Его можно оценить, определяя угол наклона дна чашки, при котором лежащие в воде на ее дне частицы начинают соскальзывать. Для семян лука это происходит при угле φ ≈ 300°, для чаинок и А-частичек -- при угле φ ≈ 450°. При вращении контакт с дном частиц, плотность которых близка к плотности жидкости, может нарушаться, что ведет к снижению трения. Поэтому при теоретическом анализе релаксации вращающейся частицы под ж будем понимать эффективный коэффициент трения, определяемый на основе данных эксперимента. Этот анализ выполнен в [1]. Сравнение с опытными данными даёт величину коэффициента трения 0,02-0,1. Эффективное динамическое значение коэффициента трения примерно на порядок меньше его статической величины. Сделанное предположение о характере трения частиц о дно не противоречит результатам проведенных опытов, но для количественного сравнения теории и эксперимента нужны независимые измерения эффективного коэффициента трения (и, конечно, более точные измерения динамики частицы, что не представляет проблемы). Мы показали, что смещение частицы к оси вращения жидкости определяется ее трением о дно. Частица останавливается в центре дна, когда жидкость еще продолжает вращаться. Она как бы выталкивает трущуюся о дно частицу туда, где вращение жидкости отсутствует и где возможно ее динамическое равновесие. Этот релаксационный процесс описывается классической гидродинамикой и не является парадоксальным. Однако коллективная релаксация системы многих частиц демонстрирует парадоксальные явления, которые мы обсудим ниже.
При раскрутке вместе с жидкостью системы из многих частиц нельзя исключить поляризации на них t-зарядов и притяжения одинаково заряженных частиц. В эффекте Коровяков суточный период вращения пятиугольного пятна осадка указывает на связь возникающей пентасимметрии с Солнцем. Можно ли наблюдать подобный или какой-то иной «чаиночный парадокс» прямо в стакане чая? В научной литературе сообщений об этом нет. И это создает интригу, ибо ежедневно совершаются миллионы опытов во время чаепития. Поэтому основной задачей опытов с вращением многих частиц в жидкости было попытаться подобрать условия опыта, при которых проявилась бы пентасимметрия центрального пятна осадка. Ясно, что при небольшом числе частиц пятен многоугольной формы ждать не следует. Возможно, поэтому при обычном чаепитии ничего экстраординарного на дне стакана не возникает. Значит, шанс наблюдать «чаиночный парадокс» появляется при достаточно большом числе частиц, которое определит эксперимент. Опыты со многими частицами проводились с использованием семян лука (В) и смесью чаинок разного размера (от едва видимых до крупинок диаметром ~0,3 см). При применении песчинок их раскручивание в чашке было неэффективным: они «не хотели» отрываться от дна и вращаться вместе с жидкостью. Поэтому опыты с плотными частицами не проводились. Целью опытов с легкими частицами был анализ формы осадочного пятна, который бы указывал на отсутствие или существование квантовых эффектов, влияющих на его конфигурацию. В опытах с примерно одинаковыми В-частицами ставилась задача проследить, как меняется процесс и время релаксации, а также форма центрального пятна при увеличении числа частиц. Были проведены две серии опытов с числами частиц N≈30 и 100. В первом случае столкновения частиц еще не являются определяющим фактором релаксации. Время остановки всех частиц составило величину tf (30) ≈ 10-12 с, тогда как первые частицы застывали в центре дна уже через время ti (100) ≈ 7-8 с. При одинаковой скорости раскрутки время остановки одного семени и 30 семян оказалось примерно одинаковым. Это свидетельствует о появлении дополнительных сил, ускоряющих радиальное смещение многочастичной системы. Пентасимметрия в форме центрального пятна
при N ≈30 не наблюдалась. tf (100) ≈ 15-20 с; Исследование формы центрального пятна проводилось в сериях опытов для системы из N≈200 семян лука и разномасштабных чаинок (максимальный диаметр ~0,3 см) с N≈ 200. Ставилась задача выяснить, влияет ли на формулу пятна следующие
факторы: Опыты дали два основных результата. Во-первых, контуры пятна практически всегда отличаются от круга и скорее похожи на многоугольники. Нередко видны углы, образованные четкими прямыми линиями сторон, но чаще стороны многоугольников имеют дефекты, а вершины углов сглажены. Подавляющее большинство многоугольников являются пятиугольниками, остальные − шестиугольники или четырехугольники. * К шестиугольникам относились и весьма редкие случаи, когда пятно более всего походило на круг. Правильные многоугольники возникают достаточно редко. Более часто можно наблюдать прямые углы. Фото некоторых пятен осадка приведены на рисунке.
Классическая гидродинамика не может описать появление многоугольных форм пятен, поэтому второй результат можно рассматривать как следствие первого. В опытах с одинаковыми В-частицами использовались три типа начального распределения. Основная часть опытов (100 опытов) проводилась, когда исходное распределение частиц задавалось бугорком (диаметром ~ 2см), образованным в предыдущем опыте. В 80% случаев форму центрального пятна можно было идентифицировать как пятиугольник, причем в ~10% опытов пятиугольник напоминал правильный. * Отметим, что соотношение между пятиугольниками, близкими к правильным и в виде «домиков», существенно менялось в разные дни. Вместе с долей «домиков» возрастала и доля квадратов. В случаях, когда однозначная идентификация многоугольников была затруднена, он относился к конкурирующим конфигурациям с весом 50%. В серии из 50 опытов использовалось начальное распределение частиц, получаемое из центрального бугорка легким покачиванием. Бугорок растекался в слой с увеличением радиуса в 2–3 раза и примерно радиально- и азимутально-однородным распределением частиц. Интересно отметить, что в центре слоя всегда возникал свободный от частиц участок. Пятиугольники образовывались снова в 80% опытов, но доля шестиугольников возросла и заметно преобладала над долей четырехугольников. Таким образом, изменение радиального распределения не повлияло на долю пятиугольников. Аналогичный результат имел место и в случае азимутально-неоднородного распределения, получаемого при соскальзывании бугорка к стенке. Семена располагались относительно направления на Солнце под углами примерно 00, 900, 1800 и 2700, и для каждого угла проводилось 10 опытов. Средняя доля пятиугольников составила 77%, шестиугольников – 19%, четырехугольников – 4%. Меньше всего (шесть) пятиугольников было при угле 00 и больше всего (десять) при угле 900, но из-за большой статистической погрешности говорить о выделенности каких-либо углов нельзя. Таким образом, начальное радиальное и азимутальное распределение частиц не влияет заметно на конфигурацию центрального пятна. В серии из 100 опытов с разномасштабными чаинками пятно диаметром ~ 2 см имело пятиугольную конфигурацию примерно в 85% случаев. Учитывая неточность метода идентификации формы, а также статистическую погрешность, можно считать, что размер и число частиц, не влияют существенно на форму пятна. В этой серии опытов шестиугольные конфигурации заметно преобладали над четырехугольными (5:1). Изменение начальной скорости вращения в ~3 раза также не повлияло на форму пятна. Более подробно остановимся на опытах в заполненном водой и закрытом крышкой прозрачном сосуде (пластмассовое ведерко), где свободная поверхность отсутствовала. Эта редакция опыта приближена в гидродинамическом аспекте к постановке опытов Коровякова. Вращение сосуду по или против часовой стрелке придавалось с помощью закручивания резинового шнура, привязанного к ручке ведерка. В качестве частиц использовались семена лука (N≈200). Их начальное распределение представляло собой кольцо, удаленное примерно одинаково от оси и стенок. Как и следовало ожидать, отсутствие свободной поверхности не повлияло заметно на конфигурацию центральных пятен. В серии из 40 опытов, по-прежнему, доминировали контуры пятиугольника (77,5%), на долю шестиугольников приходилось 20%, а на долю четырехугольников – 2,5%. Близкими к правильным оказались примерно 15% пятиугольников. Можно отметить меньший процент неоднозначно идентифицируемых форм. Однако наиболее существенное отличие, по-видимому, связано с
направлением вращения. При вращении против часовой стрелки (по
вращению Земли) пятиугольная форма возникала в 62,5% случаев, а
шестиугольная – в 32,5% (5% приходится на четырехугольную). Когда же
вращение шло по часовой стрелке, доля пятиугольников возрастала до
92,5%, остальные 7,5% приходились на шестиугольники. Однако большая
статистическая погрешность не позволяет сделать вывод о влиянии на
форму пятна направления вращений, но и не снимает такого вопроса.
Здесь целесообразно более полное исследование с использованием более
точных методик. Неоднозначность в определении формы центрального пятна безусловно
имеет место. Но изредка образующиеся четкие и правильные
многоугольники уже одним своим возникновением свидетельствуют о
проявлении симметрий, не учитываемых классической гидродинамикой.
Исходя из гидродинамической симметрии опытов с вращающейся
жидкостью, следовало бы ожидать образование центрального пятна в
виде * Очень редкое образование круговых пятен осадка говорит о том, что рассматриваемый поляризационный процесс реализуется практически всегда. Таким образом, в проделанных опытах, как и в опытах Коровякова, мы имеем дело с появлением негидродинамических сил, нуждающихся в интерпретации. *Отметим, что в классической жидкости шестиугольные ячейки Бенара появляются при возникновении конвекции, которая не связана с трением частиц о дно. Конвекция же с пятиугольными ячейками никогда не наблюдалась. Общим для обоих обсуждаемых эффектов является наличие симметрии, но в разной форме. В опытах Коровякова осадок принимал очертания правильных пятиугольников, ориентированных на Солнце. В описываемых здесь экспериментах пентасимметрия является доминирующей, но не единственной, а выделенная пространственная ориентация многоугольников отсутствует, и, как правило, они имеют неправильную форму. Рассмотрим возможную природу симметрий осадка в этих экспериментах и попытаемся понять причину различий. Для интерпретации пентасимметрии в эффекте Коровякова естественно предположить, что имеет место поляризация пяти вкусовых зарядов и гравионных полей, обусловленная внеземным фактором, главным образом, поляризационными процессами на Солнце. Частицы в каждом из пяти различных секторов правильного пятиугольника имеют одинаковые t-заряды, между которыми действуют силы притяжения. Солнце определяет азимутальное направление, относительно которого в плоскости вращения происходит формирование t-заряженных секторов и правильной пятиугольной конфигурации осадка. Выделенная ее ориентация на Солнце обуславливает наблюдаемое вращение пятиугольника относительно поверхности Земли в направлении, обратном ее вращению, с периодом одни сутки. Возможно, что какой-то вклад в поляризацию t-зарядов вносит и ближайшее к нам небесное тело – Луна. Размытость вершин пятиугольника можно связывать с воздействием вращающейся жидкости. ........ Литература. |
С.Кашницкий
|