|
КРАТКИЙ СТАНДАРТ-МИНИМУМ
КРИТИКИ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
(данный раздел ни в коем случае не подменяет полные
версии оригинальных работ, но лишь
дает тезисное представление о структуре и некоторых
направлениях критики ТО)
http://www.antidogma.ru/library/standard.html
Зачем вообще нужна критика?
Слегка гиперболизированная история из жизни: приходит
"ферматист" и говорит, что доказал Великую теорему Ферма.
Ему говорят: "Так вот же у Вас здесь ошибки!" Его ответ: "А
Вы попробуйте сами ее доказать! Раз не можете, тогда давайте
пока считать мое доказательство верным, но если кто-то
найдет БОЛЕЕ верное доказательство, я тут же отдам ему
остаток премии." Релятивисты тоже устраивают нечто вроде
зацикливания. Если кто-то их критикует, они говорят: "тогда
предложите что-то другое". Однако тем, кто предлагает
альтернативные решения они заявляют: "а у нас и так в теории
все в порядке" (что, конечно же, является ложью). Так нужно
или нет искать ошибки (хотя занятие это - очень
неблагодарное)?
1. Сколько существует вариантов теории относительности?
Речь не идет об официальном подразделении на специальную (или
частную) и общую теории относительности. Мы составим далеко не
полную таблицу с разными (взаимоисключающими) трактовками некоторых
вопросов теории относительности самими (!) релятивистами:
|
N |
Один из
вариантов ответа на конкретный вопрос в теории
относительности |
Альтернативный вариант ответа на тот же вопрос в ТО самими
релятивистами |
|
1 |
Релятивистские кинематические эффекты объективны и
наблюдаемы. |
Релятивистские кинематические явления не наблюдаемы. |
|
2* |
Для определения изменения хода времени надо использовать
прямые преобразования Лоренца. |
Для определения изменения хода времени можно использовать
обратные преобразования Лоренца. |
|
3* |
Для определения изменения длин надо использовать прямые
преобразования Лоренца. |
Для определения изменения длин можно использовать обратные
преобразования Лоренца. |
|
4 |
Скорость света не зависит только от скорости движения
источника сигнала. |
Скорость света (S/t) не
зависит также и от скорости
движения приемника. |
|
5 |
Масса зависит от скорости движения. |
“Масса есть масса” и не зависит от скорости движения. |
|
6 |
В
ОТО нет законов сохранения и это – признак ее величия. |
Надо вводить дополнительные условия и можно получить
полевую версию. |
|
7 |
Скорость света постоянна. |
Скорость света зависит от гравитации. |
Некоторые из релятивистов категорически (необоснованно) утверждают,
что наличие гравитации (или ускорений) автоматически требует
рассмотрения задачи в ОТО, другие же осознают, что это далеко не
всегда так - независимые эффекты должны суммироваться и т.д.
Очевидно, что число вариантов теории относительности составляет 2N,
где N - число строк в данной таблице (причем по ряду следствий и
вспомогательным вопросам таблица могла бы быть продолжена).
Например, из пунктов со звездочкой (2 и 3) в зависимости от того,
прямыми или обратными преобразованиями Лоренца будем пользоваться
(то есть будет находиться наблюдатель в покоящейся или движущейся
системе), можно составить следующие варианты, которые названы
О.Е.Акимовым "парадоксом штриха":
|
Вариант |
Авторы |
Изменение
длин |
Изменение
хода
времени |
|
1 |
А.
Эйнштейн; М. Борн; В. Паули |
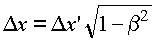 |
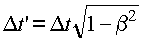 |
|
2 |
Берклеевский курс физики |
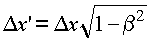 |
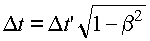 |
|
3 |
Л.Д. Ландау, Е.М. Лифшиц |
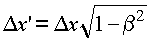 |
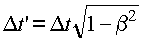 |
|
4 |
В.Г. Левич |
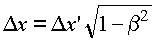 |
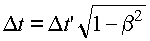 |
В этом примере релятивисты искренне не понимают элементарной
разницы: для объективно существующего мира вовсе не одно и то же -
"вы удлинились, или же ваш близнец укоротился" (перефразируя
известный анекдот про Наполеона и его длинного маршала - совсем не
одно и то же "подняться Наполеону на цыпочки, или укоротить маршала
на целую голову"). Причём релятивисты, исповедующие разные взгляды
не пытаются спорить друг с другом (по-сути, это клан, или религия;
зато они всячески пытаются стравить противников ТО между собой,
часто используя более второстепенные разногласия).
Так за какой же из огромного множества 2N вариантов воюют
релятивисты как за очередное "единственно верное учение"?
2. Ограниченность преобразований Лоренца
Совсем странно выглядит распространяемый некоторыми релятивистами
штамп, будто СТО - это просто новая геометрия и уже потому она якобы
непротиворечива. Приходится им напомнить, что физика занимается
исследованием причин явлений и конкретных механизмов,
непосредственно влияющих на исследуемое явление. Конечно, для
получения математического решения в физике часто используются
преобразования координат (например, конформные). По сути, это всего
лишь элементарные подстановки (каких существует в школьных и
студенческих задачах целое "море"). Однако если некто будет
утверждать, что, раз решения получаются верные, значит вся Вселенная
"преобразовалась" из одной области (например, круга) в другую
область, то все физики поймут, где место подобным высказываниям
(только псевдоматематику с больным воображением может прийти в
голову, что вся Вселенная сожмется, если он проделает некоторые
операции с математическими "крючками"; какая "сила" релятивистской
мысли!). И существование преобразований Лоренца в СТО вовсе не
доказывает объективность кинематических эффектов. Во-первых,
преобразования Лоренца являются не единственным, а лишь ОДНИМ ИЗ
математических инвариантов волнового уравнения. До них, например,
были открыты преобразования Фогта, также являющиеся инвариантом
волнового уравнения. Во-вторых, из самой математики не следуют
какие-либо физические принципы: свойство инвариантности полностью
определяется комбинацией операций и буковок в уравнении. В
частности, преобразования Лоренца со скоростью звука вместо скорости
света c можно использовать для некоторых акустических задач
именно потому, что они будут инвариантом (но очевидно, что ни каких
преобразований пространства при этом не наблюдается). В-третьих,
преобразования Лоренца получены для процесса распространения света в
пустоте. А это совершенно частное физическое явление и не надо
преувеличивать его общность. Заметим, что если некоторое
математическое уравнение оказывается инвариантным относительно
преобразований типа Лоренца с некоторой константой c, то это всего
навсего означает, что среди частных решений данного уравнения есть
"поверхности" волнового типа, способные распространяться со
скоростью c. При этом даже у выбранного уравнения могут быть еще и
другие частные решения со своими инвариантными преобразованиями, не
говоря уже об иных математических уравнениях, то есть для математики
никаких общематематических выводов из факта инвариантности не
следует. Только релятивисты пытаются из частного явления "раздуть
мыльный пузырь" и "клонировать" свою инвариантность на свойства
всего мира. Никто же не делает общевселенские выводы из инвариантов
уравнения теплопроводности для водорода или свойств водородной
плазмы только на том основании, что все атомы имеют в своем составе
электроны, а ядра - протоны. Вся Вселенная "кричит", что ее
симметрии не совпадают с примитивной сферической симметрией точечных
световых вспышек в пустоте (посмотрите на кристаллы, на живые
существа, на Космос). По одной скалярной константе c невозможно
определить даже скорость света в реальных веществах (конкретных
газах, жидкостях, кристаллах), не говоря уже о том, что возмущения в
среде вообще распространяются со скоростью звука. Эта последняя
скорость тоже не детерминируется одной константой, а зависит от
конкретного вещества (может, например, быть анизотропной).
По-видимому, вообще подогнать все свойства мира под одну схему
инвариантности невозможно. Даже для процесса распространения света
кроме "свойств" пустоты в процесс вовлечены элементы среды (атомы и
молекулы), обладающие огромным разнообразием свойств, и вовлечено
взаимодействие с приборами, что сразу индивидуализирует процесс
(т.е. должно быть как минимум нечто среднее между свойствами пустоты
и свойствами конкретного вещества). Теперь о математическом выводе
преобразований Лоренца (точнее об одном из более-менее
корректных способов). Ищется такое преобразование, которое переводит
уравнение одной сферы (иногда интервала) в уравнение другой сферы
(соответственно, другого интервала). Очевидно, что для четырех
переменных такое преобразование не единственное. Во-первых,
отдельное приравнивание Y=Y1, Z=Z1 представляет собой лишь
одну из возможных гипотез, также как и требование линейности,
взаимной однозначности, обратимости и т.д.. (Например, элементарно
вместо константы c включить в преобразования разные
функциональные зависимости.) Во-вторых, любое преобразование
световых поверхностей вовсе не детерминирует преобразование объемов (в
которых могут происходить неэлектромагнитные физические процессы).
Напомним, что скорость звука тоже не зависит от движения источника,
но никаких глобальных выводов о свойствах пространства и времени
отсюда не следует. Таким образом, совершено частные преобразования
(Лоренца) не могут накладывать каких-либо ограничений на всю физику.
3. Противоречивость релятивистского понятия времени
Предварительно напомним, что в классической физике результаты,
полученные одним из наблюдателей, могут быть использованы любым
другим наблюдателем (то есть верны для всех). Поэтому наша цель -
сформулировать такую симметричную постановку задачи, чтобы ответ был
очевиден из здравого смысла. Релятивисты же, публично отрекшиеся от
здравого смысла, должны рассмотреть результаты (разные) с точки
зрения всех наблюдателей, участвовавших в эксперименте и сопоставить
их между собой, чтобы доказать отсутствие противоречий и наблюдаемость своих
релятивистских эффектов. Однако почему-то они этого никогда не
доделывают до конца. Та же хитрость наблюдается при "отписке" на
необходимость использования диаграмм (хотя неужели кто-то из них
будет утверждать, что преобразования Лоренца недостаточны, а
диаграммы дают нечто большее?): релятивисты не исследуют свои
решения на предмет отсутствия противоречий с точки зрения всех наблюдателей.
Еще одно предварительное замечание (хотя и очевидное) касается
аддитивности и непрерывности времени (и неразрывной связи
материальных объектов с пространством и временем). Если наблюдатель
непрерывно двигался по участкам траектории 1,2,3,..., то его возраст
изменился на 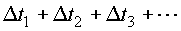 Далее,
наука физика, как правило, имеет дело с объективными измеряемыми
величинами. Одним из проявлений объективности является то, что мы
можем сопоставлять однотипные величины, даже если объекты, над
которыми проводились измерения, не существовали одновременно (так,
мы можем, в принципе, сравнить вес немецкой овчарки с весом
бронтозавра, или среднюю продолжительность жизни дриопитека со
средней продолжительностью жизни американца 21 века, хотя они
никогда не встречались друг с другом). Поэтому при сопоставлении
времён движения по двум разным траекториям вовсе нет никакой
необходимости не только в синхронизации часов (ну нет такого ЗАКОНА
В МАТЕМАТИКЕ, чтобы сопоставление цифр между собой требовало
некоторой выдуманной Эйнштейном псевдофизической процедуры!), но
даже чтобы эти движения начинались или проходили одновременно (по
одной траектории кто-то мог пролететь миллиард лет назад, а по
другой - сейчас, и затраченные времена можно сравнить). Поэтому,
можно, например, отдельно сравнивать затраченное время на участках
ускоренного движения двух близнецов и отдельно сравнивать времена,
затраченные близнецами на участках прямолинейного и равномерного
движения. Далее,
наука физика, как правило, имеет дело с объективными измеряемыми
величинами. Одним из проявлений объективности является то, что мы
можем сопоставлять однотипные величины, даже если объекты, над
которыми проводились измерения, не существовали одновременно (так,
мы можем, в принципе, сравнить вес немецкой овчарки с весом
бронтозавра, или среднюю продолжительность жизни дриопитека со
средней продолжительностью жизни американца 21 века, хотя они
никогда не встречались друг с другом). Поэтому при сопоставлении
времён движения по двум разным траекториям вовсе нет никакой
необходимости не только в синхронизации часов (ну нет такого ЗАКОНА
В МАТЕМАТИКЕ, чтобы сопоставление цифр между собой требовало
некоторой выдуманной Эйнштейном псевдофизической процедуры!), но
даже чтобы эти движения начинались или проходили одновременно (по
одной траектории кто-то мог пролететь миллиард лет назад, а по
другой - сейчас, и затраченные времена можно сравнить). Поэтому,
можно, например, отдельно сравнивать затраченное время на участках
ускоренного движения двух близнецов и отдельно сравнивать времена,
затраченные близнецами на участках прямолинейного и равномерного
движения.
Начнем с традиционного парадокса близнецов. Многие релятивисты для
его "объяснения" привлекают ускорение одного из близнецов. Напомним,
что без ускорения согласно СТО, по мнению каждого брата, другой
должен оказаться более молодым. Однако, из Рисунка видно, что
участки с ускорениями |OA| и |BC| можно зафиксировать одинаковыми по
величине, но для разных случаев i произвольно менять расстояние |AB|
полета с постоянной по модулю большой скоростью, например, выбирать
это расстояние в 3, 5, ... раз больше первоначального.
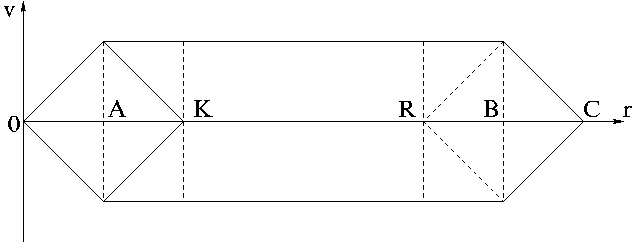
Ясно, что одно и то же ускорение не сможет
для всех этих разных случаев объяснить различную разницу 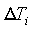 в
возрасте близнецов. Более того, брат-домосед может не полениться и
“принять участие” только в ускоренных движениях на участках |OA| и
|AK|, полностью идентичных тем, что имеются у брата-космонавта
(стартуя в расчетный момент пролета точки R братом-космонавтом).
Таким образом, первоначальное “объяснение” парадокса близнецов с
помощью ускорения, которого придерживались Эйнштейн, Паули, Борн и
другие, можно сдать в пыльный архив как не имеющее научной ценности. в
возрасте близнецов. Более того, брат-домосед может не полениться и
“принять участие” только в ускоренных движениях на участках |OA| и
|AK|, полностью идентичных тем, что имеются у брата-космонавта
(стартуя в расчетный момент пролета точки R братом-космонавтом).
Таким образом, первоначальное “объяснение” парадокса близнецов с
помощью ускорения, которого придерживались Эйнштейн, Паули, Борн и
другие, можно сдать в пыльный архив как не имеющее научной ценности.
Вначале докажем вспомогательное утверждение (не имеющее прямого
отношения к СТО), что наличие взаимных ускорений космонавтов не
может привести к разнице в ходе времени. Проще всего это сделать с
помощью двух идентичных траекторий-петель, изображенных на Рисунке.
Космонавты стартуют из одной точки, одинаковым образом ускоряются на
данных петлях до одинаково больших скоростей и опять пролетают
одновременно через одну точку. Естественно, вследствие симметрии
задачи изменения в их возрасте за время разгона будут одинаковыми,
что подтвердит наблюдатель в точке старта (этот очевидный из
здравого смысла результат должен быть одинаков, независимо от
теории, в которую вы верите и по которой хотите считать).
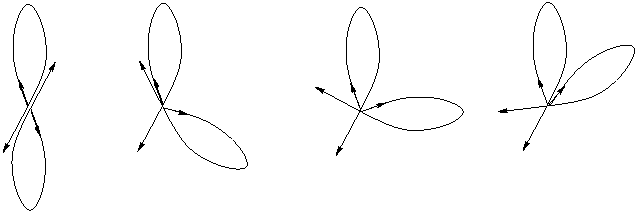
Напомним, что ускорение – величина векторная. Мы
можем одну из траекторий-петель повернуть без изменения ее формы
относительно точки старта на любой угол, и, хотя в каждом таком
случае относительные ускорения космонавтов будут различаться, их
возраст в любом из случаев изменится на одну и ту же величину. Это
проявление свойства изотропии пространства. Очевидно также, данные
траектории-петли можно параллельно (без изменения формы) переносить
в пространстве, и "набег" времени от движения по петлям при таком
переносе не изменится. Подобные одинаковые траектории-петли могут
быть использованы для ускорения, для разворота и для замедления
космонавтов. Кроме того, ускорения можно выбрать по величине равными
ускорению свободного падения на Земле, чтобы "несущественная роль
участков с ускорением" была понятна даже с точки зрения верующих в
ОТО.
Теперь, к нарисованым ранее двум петлям мы можем пристыковать
одинаковые прямолинейные участки для движения с одинаковой
постоянной скоростью (и выбрать длину таких участков намного большей
длины петель). На концах этих отрезков можно пристыковать одинаковые
разворотные петли. Таким образом, космонавты одинаково разгоняются
(t1=t1'), пролетают после прекращения
ускорения через одну точку, летят с постоянными, одинаковыми по
модулю скоростями, одинаково разворачиваются (t3=t3'),
летят обратно с постоянными, одинаковыми по модулю скоростями и
замедляются одинаковым образом (t5=t5') по
прежним разгонным петлям. Вследствие симметрии задачи с точки зрения
классической физики (здравого смысла, что называется "по жизни";
впрочем, такой результат должен быть и с точки зрения любой другой
теории) возраст космонавтов-близнецов будет очевидно одинаковым TI=TII.
Но TI=t1+t2+t3+t4+t5,
а TII=t1'+t2'+t3'+t4'+t5'.
Опять траекторию одного из близнецов (II) можно повернуть на
произвольный угол относительно близнеца I вокруг точки старта O (см.
Рисунок).
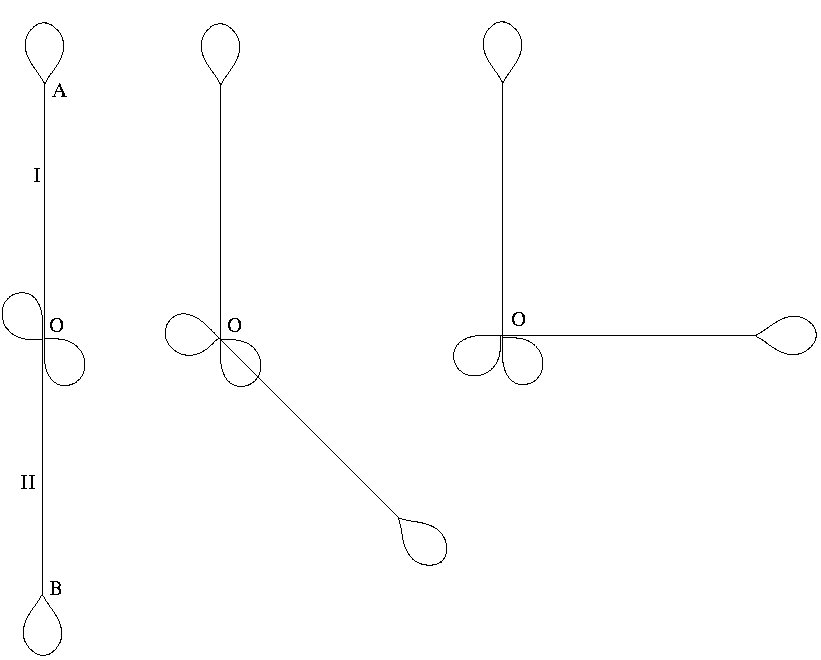
Ранее мы показали, что участки с ускорением
(петли) не влияют на результат сравнения возраста космонавтов.
Значит, нам осталось только для участков равномерного прямолинейного
движения сравнить величины t2 с t2' и t4 с
t4' (а эта задача уже "лежит чисто в зоне
ответственности" СТО). Однако, вследствие векторного характера
скорости, их относительная скорость изменится при повороте
траектории, то есть согласно СТО с точки зрения каждого из
космонавтов должен поменяться возраст, что очевидно нелепо
(противоречит изотропии пространства).
Противоречивость релятивистского понятия времени можно доказать еще
короче. Пусть для близнецов (двух или более) точка старта (начало
эксперимента) - одна и та же, и пусть их встреча тоже состоится в
одной точке. Поскольку в формулу замедления времени входит только
лишь квадрат относительной скорости, то с точки
зрения любого из близнецов ненулевой (относительной) скорости
другого близнеца уже достаточно, чтобы возраст другого близнеца стал
меньше. И так должно было бы быть с точки зрения любого из
близнецов, что, очевидно, невозможно.
Напомним также аргументы президента Королевского астрономического
общества, профессора Герберта Дингла: 1) Согласно самому принципу
относительности, при разъединении и последующем воссоединении
близнецов, никакой наблюдаемый эффект, демонстрирующий абсолютным
образом наличие движения только одного из них, не может иметь места;
2) если после воссоединения одни из двух идентичных часов,
участвовавших в относительном движении, отстанут, то это будет
свидетельствовать о движении лишь данных часов; 3) таким образом,
если верен принцип относительности, то показания обоих часов после
воссоединения должны быть одинаковыми, если они были одинаковы до
разъединения.
Многочисленные другие логические противоречия релятивистского
понятия времени также доказывают его полную несостоятельность.
В своих агитациях за ТО релятивисты совершают
следующие два преднамеренных подлога. Во-первых, они
умышленно пытаются создать иллюзию, будто время и часы -
это одно и то же. Задолго до СТО-шных выдумок, когда выверенные часы
из Европы попали на Экватор, оказалось, что они стали сильно
отставать, причём это были не мифические наносекунды, а величины,
заметные практически за сутки. Слава Богу, что ни одному идиоту,
если они тогда были, не пришло в голову, что время на Экваторе идет
"настолько существенно по-другому". Естествоиспытатели сразу же
определили конкретный физический механизм, влияющий на конкретное
устройство часов. Точность часов, высокая или низкая, также не имеет
никакого отношения к самому ходу времени!
Во-вторых, релятивисты умышленно пытаются создать мнение, будто синхронизация
времени и обмен сигналами в процессе опыта - это одно и
то же. Так, при введении григорианского календаря была произведена
синхронизация времени. Но никто при этом не изобретал машину
времени, не летал сообщать Александру Македонскому, в каком году до
Рождества Христова он родился и т.д.. Просто, если некое "физическое
понятие" претендует на "научность", то для него всегда существуют
математические формулы и методы пересчёта. И синхронизация может
быть проведена либо до, либо во время, либо после опыта, либо,
вообще, методом пересчёта. Так, для всех мысленных опытов СТО с
двумя "объектами" существует взаимно однозначная математическая
связь классических представлений с релятивистскими. Это отлично
понимал А. Пуанкаре, считая новые понятия и преобразования лишь
одним из ! возможных "соглашений", наравне ! с прежними
классическими понятиями (см. в книге А.Пуанкаре "О науке", работу
"Последние мысли", главу II и комментарии в конце книги в статье
М.И.Панова, А.А.Тяпкина и А.С.Шибанова). А вот при описании
пространственного движения с числом объектов больше двух "новые
понятия" СТО часто дают осечки.
4. Противоречивость релятивистского сокращения расстояний
Поскольку СТО создавалась как "игра со световыми зайчиками Эйнштейна
в абсолютно пустом пространстве", то любые псевдопарадоксы с
использованием электромагнитного поля (токов с контактами, лазеров,
световых лучей с зеркалами и т.д.) легко разрешимы, и релятивисты
хитро преподносят их как якобы отсутствие противоречий в СТО. Для
этого они просто совершают подмену и вместо реальных парадоксов
"разбирают" такие выдуманные или "дополненные" ими псевдопарадоксы
со всякими электрическими контактами, якобы эффектными взрывами и
т.д. Так что будьте внимательны к такому подлогу! А теперь
рассмотрим конкретные парадоксы сокращения длин. Пусть на твердой
плоскости лежит тонкая пластина больших размеров, из которой вырезан
небольшой крест:
Парадокс креста.
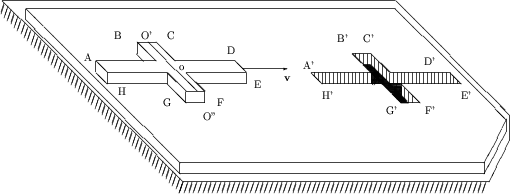 |
Пусть длина креста много больше ширины
перекладины |AD| >> |BC|. Пусть крест скользит горизонтально по
пластине так, чтобы в классической физике он занял свою нишу
(например, упал в нее под действием любой силы, например, силы
тяжести). Выберем относительную скорость движения v такую,
чтобы согласно релятивистским формулам длина сокращалась в два раза
(или более). Заметим, что центр тяжести креста (точка o) находится
также и в центре перекладины. Следовательно, вертикальное движение
креста (падение или поворот переднего конца) возможно только, если:
(1) центр o и вся центральная линия перекладины (O'O") находятся над
пустым пространством, и (2) ни одна из точек C, D, E, F не имеет
опоры. С точки зрения наблюдателя на кресте он проскользнет
укоротившуюся в два раза нишу, так как всегда на пластину опирается
либо перекладина и один из концов, либо оба конца. Известный фокус с
поворотом стержня (к которому релятивисты упорно пытаются свести
парадоксы сокращения длин) здесь не проходит. Однако, с точки зрения
наблюдателя на пластине крест (ставший в два раза меньше) упадет в
нишу. Таким образом, мы имеем два различных события: так было ли
падение (толчок о плоскость) или нет?
Следующее замечание. Поскольку сокращение длин объектов связывают со
свойствами самого пространства, то сокращаться должно также и
расстояние до объекта (независимо от того, приближаемся мы к объекту
или удаляемся от него!). Следовательно, при достаточно большой
скорости ракеты (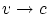 )
мы можем не только рассматривать удаленные звезды, но и дотронуться
до них рукой, ведь в нашей собственной системе отсчета наши размеры
не меняются. Кроме того, улетая от Земли в течение длительного
времени с большим ускорением (СТО не накладывает ограничений на
ускорение), мы окажемся от нее на расстоянии "одного метра". В какой
же момент наблюдатель, находящийся на расстоянии этого самого
"одного метра" увидит реверсное (то есть обратное - против действия
реактивных двигателей) движение ракеты? )
мы можем не только рассматривать удаленные звезды, но и дотронуться
до них рукой, ведь в нашей собственной системе отсчета наши размеры
не меняются. Кроме того, улетая от Земли в течение длительного
времени с большим ускорением (СТО не накладывает ограничений на
ускорение), мы окажемся от нее на расстоянии "одного метра". В какой
же момент наблюдатель, находящийся на расстоянии этого самого
"одного метра" увидит реверсное (то есть обратное - против действия
реактивных двигателей) движение ракеты?
Рассмотрим теперь парадокс распиленной линейки (предварительно
вспомните метод деления целого на части в доказательстве Галилея о
том, что нет причин ускорению свободного падения увеличиваться в два
раза при увеличении массы падающего тела в два раза). На рисунке
изображены 4 идентичные линейки. Линейка A лежит неподвижно на
старте в качестве эталона. Линейка B лежит неподвижно на финише в
качестве эталона (обе эти линейки изображены исключительно для
наглядности). Линейка C будет во время эксперимента двигаться. Она
распилена на две равные части 1 и 2. Линейка D тоже будет во время
эксперимента двигаться, но она не распилена. Рассмотрим отдельно
движение первой половинки-1 линейки C: пусть она начинает двигаться
с равномерным ускорением, достигает большой заданной скорости V,
летит с такой постоянной скоростью и своим правым концом пересекает
финишную прямую F. Если вторая половинка-2 линейки C начала
двигаться в тот же момент, что и первая половинка-1, двигалась с тем
же равномерным ускорением до достижения той же скорости V,
а затем с такой же постоянной скоростью летела дальше, то ее
местоположение к моменту пересечения финиша первой половинкой
линейки - она будет пересекать линию O', как изображено на рисунке:

Этот результат очевиден, поскольку ситуация со
второй половинкой линейки отличается от ситуации с первой половинкой
линейки только лишь параллельным переносом начала координат (правого
конца половинки линейки с линии S на линию O). Однако, для
нераспиленной линейки D ситуация с финишем будет иной (линейка
изображена на Рисунке достигшей финиша как целое). Имеем логическое
противоречие. Во-первых, откуда линейка C могла знать, что она
распилена? Во-вторых, распил нулевого размера не мог согласно СТО
превратиться в ненулевой пространственный зазор. Противоречие
невозможно устранить, даже если объявить о неравноправии систем
отсчета и необходимости иметь преимущественную систему с
определенным расположением начала координат (т.е. пожертвовать самой
относительностью!): ведь линейку можно распилить на 3 и более частей
и спасая один из распилов, остальные распилы все равно образуют при
движении ненулевые зазоры.
Рассмотрим теперь другой пространственный парадокс, связанный с
якобы существующим релятивистским поворотом стержня. Напомним
задачу, когда тонкий стержень некоторой длины L летит вдоль оси X со
скоростью v, а пластина с нишей того же размера L наезжает со
скоростью V в направлении оси Z так, чтобы в классическом
случае стержень точно прошел в нишу (см. Рисунок). Релятивисты
“устраняют” противоречия в показаниях разных наблюдателей путем
введения релятивистского поворота стержня. Однако ситуацию с
релятивистским углом поворота стержня элементарно сделать
драматичной, ведь он однозначно зависит от отношения скоростей.
Пусть по нашему стержню скользит с некоторой скоростью другой,
меньший стержень l. Наблюдатели на обоих стержнях будут
утверждать, что зазора между стержнями нет. Однако, вследствие
разной скорости стержней (v и v1),
для наблюдателя на пластине большой стержень L и малый стержень l должны,
согласно СТО, быть повернутыми на разные углы относительно
пластины. То есть малый стержень в СТО будет повернут вверх
относительно большого стержня и между стержнями появляется зазор.
Имеем очевидное противоречие.
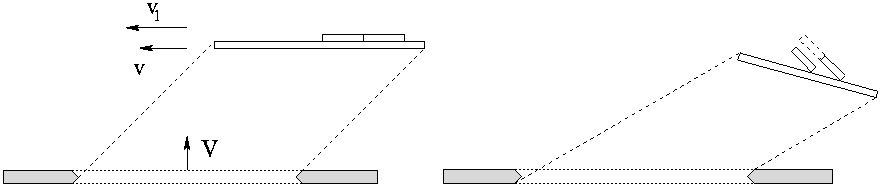
Это противоречие можно сделать еще более
выпуклым, если воспользоваться идеологией деления целого на части
(примененной впервые Галилеем при доказательстве независимости
ускорения свободного падения от массы падающего тела; см. выше
парадокс распиленной линейки). Тогда, если считать стержень l единым
целым, то получается одна ситуация (см. Рисунок), будто бы вторая
половина стерженька приподнята на некоторую высоту над стержнем, по
которому происходит скольжение. Но если считать стерженек состоящим
из реальных двух половинок, то данная ситуация для второй половинки
стержня просто аналогична случаю переноса начала координат и эти
половинки оказываются передними концами на большом стержне, но
пространственно разделенными (см. Рисунок). Последняя ситуация
особенно странная, так как разрез нулевого размера при любых
поворотах или умножениях на релятивистский коэффициент должен
оставаться нулевым. Заметим, что мы еще немного "подыграли" СТО,
повернув малые стержни НАД большим. На самом деле в СТО вовсе нет
реальных твердых тел, непроницаемых друг для друга. Ведь все
(!) формулы СТО получены с использованием вспышек света, а вспышки
света способны беспрепятственно проходить друг сквозь друга. В
результате для согласования с показаниями наблюдателя в центре
стерженька, остается предположить, будто один стержень проходит
сквозь другой (абсурдное несоответствие модели реальности).
Таким образом, представления теории относительности приходят в
противоречие с таким важным и проверенным элементом понятия
относительность как однородность пространства (возможность
параллельного переноса начала координат). Наличие других
дополнительных многочисленных логических противоречий делает
невозможным конструктивное использование релятивистского понятия
длины.
5. Противоречивость релятивистского понятия "относительность
одновременности"Разберем мысленный
эксперимент, "демонстрирующий" относительность одновременности:
пусть вспышка света происходит в момент совпадения центров O и O'
движущихся друг относительно друга систем S и S' в точке O=O'.
Согласно СТО за время 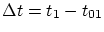 по
часам системы S свет пройдет расстояние по
часам системы S свет пройдет расстояние 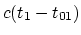 от
центра O. За такое же время от
центра O. За такое же время 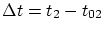 по
часам системы S' тот же свет пройдет расстояние по
часам системы S' тот же свет пройдет расстояние 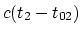 от
центра O'. Согласование начальных времен не влияет на разность
времен и может быть проведено как до эксперимента, так и после него
любым методом. Можно заранее договориться о вспышках по часам
системы S (например, периодически каждый миллион лет), а систему S'
"организовать" за мгновение до выбранной заранее вспышки. Вспомним,
что основная положительная идея СТО состояла в конечности скорости
передачи взаимодействий. Эту же идею выражает теория близкодействия
и отражает полевой подход (через уравнения Максвелла): световой
фронт от источника до приемника проходит последовательно все
промежуточные точки пространства. Именно с этим свойством приходит в
противоречие понятие относительности одновременности. от
центра O'. Согласование начальных времен не влияет на разность
времен и может быть проведено как до эксперимента, так и после него
любым методом. Можно заранее договориться о вспышках по часам
системы S (например, периодически каждый миллион лет), а систему S'
"организовать" за мгновение до выбранной заранее вспышки. Вспомним,
что основная положительная идея СТО состояла в конечности скорости
передачи взаимодействий. Эту же идею выражает теория близкодействия
и отражает полевой подход (через уравнения Максвелла): световой
фронт от источника до приемника проходит последовательно все
промежуточные точки пространства. Именно с этим свойством приходит в
противоречие понятие относительности одновременности.
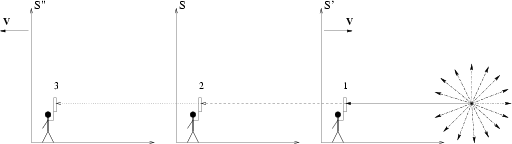
Для доказательства этого мы воспользуемся двумя
утверждениями из СТО: 1) одна и та же вспышка света одновременно
достигает движущихся друг относительно друга наблюдателей, несмотря
на то, что за время прохождения света наблюдатели пространственно
разойдутся друг от друга на некоторое расстояние; 2) кинематические
формулы СТО (из учебников) содержат только квадрат скорости. Пусть,
например, первый наблюдатель в системе S' движется по направлению к
источнику вспышки с малой скоростью. Поскольку расстояние до точки
вспышки велико (миллион световых лет), то за миллион лет оба
наблюдателя разойдутся на большое расстояние. По формулам СТО время
прихода сигнала для каждого наблюдателя будет одинаковым. В какой же
точке пространства первый наблюдатель "прозевал" световой фронт для
второго наблюдателя? А если бы он весь миллион лет держал зеркало, а
за 1 секунду до приема сигнала убрал его? По-мнению второго
наблюдателя сигнал отражен первым наблюдателем где-то впереди. А что
отражал первый наблюдатель, если его приборы еще не реагировали на
вспышку? Аналогично, третий наблюдатель может удаляться от второго с
той же скоростью, но направленной от источника. Увидит ли третий
наблюдатель свет, если второй будет держать зеркало миллион лет без
одной секунды? С одной стороны, поскольку в формулы СТО входит
только квадрат скорости, то второй наблюдатель будет считать
одинаковым время получения сигнала первым и третьим наблюдателем.
Можно договориться об отправлении без задержек дополнительно своих
сигналов при получении каждым наблюдателем исследуемого сигнала.
Тогда, если расчеты второго наблюдателя верны, он должен
одновременно получить дополнительные сигналы от первого и третьего
наблюдателей (задача ведь симметрична). Однако, с другой стороны,
согласно уравнениям Максвелла свет распространяется непрерывно и
второй наблюдатель получит дополнительный сигнал от первого
наблюдателя одновременно с тем, как и сам увидит исследуемый сигнал.
По-мнению второго наблюдателя свет к этому времени еще не дошел до
третьего наблюдателя. Таким образом, второй наблюдатель приходит в
противоречие сам с собой: первые расчеты по формулам СТО
противоречат вторым расчетам по уравнениям Максвелла. Очевидно, что
вспышку наблюдатели увидят не одновременно, а последовательно,
поскольку пространственный путь света един: источник, первый
наблюдатель, затем второй, и, наконец, третий наблюдатель.
Таким образом, релятивистская "относительность одновременности" не
отвечает реальности.
6. Сводимость релятивистского уравнения движения к уравнению
НьютонаРелятивистское уравнение движения с
силой Лоренца F элементарно может быть записано как
классический второй закон Ньютона с некоторой другой силой F'.
Для этого надо в левой части релятивистского уравнения 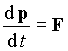 в
явном виде найти производную от релятивистского импульса, умножить
скалярно левую и правую части уравнения на v. Тогда
получается соотношение в
явном виде найти производную от релятивистского импульса, умножить
скалярно левую и правую части уравнения на v. Тогда
получается соотношение
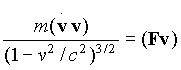 . .
Подставляя его в первоначальное релятивистское
уравнение движения, получаем второй закон Ньютона с силой F' в
правой части:
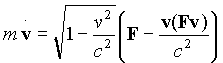 . .
Неужели релятивисты не знакомы с механикой и
гидродинамикой, когда в самой что ни на есть нерелятивистской
области скоростей силы оказываются зависящими от скорости движения
тел (может вводиться понятие присоединенной массы и т.д.). Так есть
ли что-нибудь "великое" в подобной "новой" релятивистской
зависимости силы от скорости? Конечно же - нет! Формально в данном
выражении силы F' в качестве буквы Fможет
стоять любая сила, однако нет никаких доказательств, что
релятивистское уравнение движения применимо к чему-либо, кроме
заряженных частиц, находящихся под действием силы Лоренца. При этом
считается, что силы преобразуются при переходе от одной системы к
другой. Вообще говоря, сама идея преобразования сил при переходе от
одной системы наблюдения к другой системе представляет собой нонсенс
для всей экспериментальной физики. Действительно, написание арабских
цифр на динамометре не зависит от движения наблюдателя, то есть
показания динамометра, фиксирующего силу, не изменятся от движения
глаз наблюдателя. Сила действует между "источником" этой силы и
конкретным "объектом" ее приложения, а движение каких-то посторонних
глаз наблюдателя здесь совершенно не при чем (т.е. сила может
определяться только свойствами источника, объекта и их взаимным движением).
Экспериментальные уравнения движения полностью определяют и
все характеристики движения, в том числе, первые интегралы движения
(энергию и импульс, которые в данном случае будут отличаться от
выражений для модели невзаимодействующих материальных точек).
Теперь сделаем несколько замечаний об уравнениях Максвелла. Разберем
вначале "принципиальный" вопрос об инвариантности уравнений
Максвелла, широко эксплуатируемый в СТО. В учебнике Сивухина к
системе фундаментальных уравнений электродинамики относятся
следующие четыре уравнения (в дифференциальной форме):
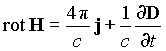 , , 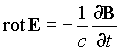 , ,
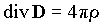 , , 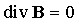 . .
Однако эта система восьми уравнений (в
координатной форме) очевидно недостаточна для определения 16-ти
компонент величин E, D, B, H, j и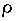 .
Необходимо, также ввести в уравнения характеристики среды. С учетом
существования нелинейных, неоднородных, неизотропных сред сделать
это в общем виде не представляется возможным. Только в определенных
пределах можно ввести частные модельные представления о линейных
зависимостях: .
Необходимо, также ввести в уравнения характеристики среды. С учетом
существования нелинейных, неоднородных, неизотропных сред сделать
это в общем виде не представляется возможным. Только в определенных
пределах можно ввести частные модельные представления о линейных
зависимостях: 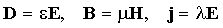 и
добавить еще 9 уравнений с тремя новыми неизвестными функциями и
добавить еще 9 уравнений с тремя новыми неизвестными функциями 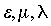 (или
постоянными – для модельных задач), характеризующими среду. О единой
инвариантности последних трех уравнений не может идти и речи.
Напомним, например, о существовании ферромагнетиков и
сегнетоэлектриков, для которых наблюдаются явления гистерезиса, то
есть ход процесса зависит от его предыстории. В последних случаях
поведение вообще не описывается дифференциальными уравнениями. Можно
ли “раздувать мыльный пузырь СТО” только на инвариантности части из
полной системы уравнений? Очевидно, нет! Так можно было бы из любого
уравнения выделить произвольные кусочки и спекулировать на
инвариантности этих слагаемых. Таким образом, система уравнений
Максвелла в произвольных средах не может быть инвариантной
относительно какого-то единого физического преобразования. Первые
четыре уравнения Максвелла могут представлять самостоятельный
интерес только при рассмотрении полей в пустоте. Однако
инвариантность уравнений Максвелла в пустоте относительно
преобразований Лоренца совершенно ничего не означает для других
явлений. Во-первых, в пустом пространстве мы можем отрезать половину
отрезка и увеличить ее вдвое – получим такой же отрезок. Поэтому в
пустом математическом пространстве можно пользоваться любыми
системами отсчета, непротиворечивыми геометриями и переводными
коэффициентами. Это может определяться только лишь удобством
математического описания. Однако наличие в пространстве реальных
физических тел и полей задает естественные реперные точки,
характерные масштабы и взаимосвязи между объектами. Все это
определяет отличия реального физического пространства от
пустого математического пространства. Во-вторых, свойство некоторых
взаимодействий распространяться в вакууме со скоростью света не
детерминирует скорость распространения взаимодействий в среде.
Несмотря на огромную роль электромагнитных взаимодействий,
возмущения в средах распространяются со скоростью звука. По одной
константе c, относящейся к вакууму, невозможно определить
(для нашего "электромагнитного" мира) скорости звука и света в
средах: например, не всякой частоты свет может распространяться в
веществе (напомним про рассеяние, поглощение, затухание, отражение).
Все эти и многие другие свойства (например, анизотропия) выходят за
пределы применимости уравнений Максвелла в пустоте. Следовательно,
подгонять свойства всего мира под инвариантность уравнений Максвелла
в пустоте – слишком завышенная претензия СТО. В-третьих, разбиение
единого по своему действию поля на электрическую и магнитную части
довольно условно и инвариантность этих искусственно выделенных
частей не может иметь решающего значения. Важное замечание. Сами по
себе уравнения Максвелла могут приобрести физический смысл только
после того, как будет указан физический способ измерения введенных
характеристик полей. На сегодняшний день таким “замыкающим
уравнением” является уравнение движения заряженных частиц под
действием силы Лоренца. Напомним, что в разные периоды времени в
качестве электромагнитной силы сила Лоренца была не единственной.
Среди наиболее известных выражений были: сила Ампера, сила Вебера и
многие другие. Если бы современная электродинамика имела
самосогласованный характер, то, поскольку поля проявляются по их
силовому воздействию, выражение для электромагнитной силы должно
было бы выводиться из уравнений Максвелла, а не вводиться
искусственно. Такое выражение было получено И.И. Смульским и оно
отличается от выражения силы Лоренца. Можно ли считать выражение для
силы Лоренца принципиально строгим и непротиворечивым в качестве
электромагнитной силы? По-видимому, нет! Хотя достижения современной
электродинамики общеизвестны, надо отметить и некоторые спорные
моменты. Во-первых, даже в современной электродинамике дополнительно
вводится торможение излучением, которое, однако, приводит к
бессмысленному самоускорению зарядов (ограничиваемому лишь постулативно путем
наложения условий на величины полей). Во-вторых, само возникновение
квантовой механики говорит о том, что сила Лоренца не описывает
адекватно поведение зарядов на атомных масштабах. В-третьих, для
известного явления дрейфа частиц несколько странно, что его
скорость (или
постоянными – для модельных задач), характеризующими среду. О единой
инвариантности последних трех уравнений не может идти и речи.
Напомним, например, о существовании ферромагнетиков и
сегнетоэлектриков, для которых наблюдаются явления гистерезиса, то
есть ход процесса зависит от его предыстории. В последних случаях
поведение вообще не описывается дифференциальными уравнениями. Можно
ли “раздувать мыльный пузырь СТО” только на инвариантности части из
полной системы уравнений? Очевидно, нет! Так можно было бы из любого
уравнения выделить произвольные кусочки и спекулировать на
инвариантности этих слагаемых. Таким образом, система уравнений
Максвелла в произвольных средах не может быть инвариантной
относительно какого-то единого физического преобразования. Первые
четыре уравнения Максвелла могут представлять самостоятельный
интерес только при рассмотрении полей в пустоте. Однако
инвариантность уравнений Максвелла в пустоте относительно
преобразований Лоренца совершенно ничего не означает для других
явлений. Во-первых, в пустом пространстве мы можем отрезать половину
отрезка и увеличить ее вдвое – получим такой же отрезок. Поэтому в
пустом математическом пространстве можно пользоваться любыми
системами отсчета, непротиворечивыми геометриями и переводными
коэффициентами. Это может определяться только лишь удобством
математического описания. Однако наличие в пространстве реальных
физических тел и полей задает естественные реперные точки,
характерные масштабы и взаимосвязи между объектами. Все это
определяет отличия реального физического пространства от
пустого математического пространства. Во-вторых, свойство некоторых
взаимодействий распространяться в вакууме со скоростью света не
детерминирует скорость распространения взаимодействий в среде.
Несмотря на огромную роль электромагнитных взаимодействий,
возмущения в средах распространяются со скоростью звука. По одной
константе c, относящейся к вакууму, невозможно определить
(для нашего "электромагнитного" мира) скорости звука и света в
средах: например, не всякой частоты свет может распространяться в
веществе (напомним про рассеяние, поглощение, затухание, отражение).
Все эти и многие другие свойства (например, анизотропия) выходят за
пределы применимости уравнений Максвелла в пустоте. Следовательно,
подгонять свойства всего мира под инвариантность уравнений Максвелла
в пустоте – слишком завышенная претензия СТО. В-третьих, разбиение
единого по своему действию поля на электрическую и магнитную части
довольно условно и инвариантность этих искусственно выделенных
частей не может иметь решающего значения. Важное замечание. Сами по
себе уравнения Максвелла могут приобрести физический смысл только
после того, как будет указан физический способ измерения введенных
характеристик полей. На сегодняшний день таким “замыкающим
уравнением” является уравнение движения заряженных частиц под
действием силы Лоренца. Напомним, что в разные периоды времени в
качестве электромагнитной силы сила Лоренца была не единственной.
Среди наиболее известных выражений были: сила Ампера, сила Вебера и
многие другие. Если бы современная электродинамика имела
самосогласованный характер, то, поскольку поля проявляются по их
силовому воздействию, выражение для электромагнитной силы должно
было бы выводиться из уравнений Максвелла, а не вводиться
искусственно. Такое выражение было получено И.И. Смульским и оно
отличается от выражения силы Лоренца. Можно ли считать выражение для
силы Лоренца принципиально строгим и непротиворечивым в качестве
электромагнитной силы? По-видимому, нет! Хотя достижения современной
электродинамики общеизвестны, надо отметить и некоторые спорные
моменты. Во-первых, даже в современной электродинамике дополнительно
вводится торможение излучением, которое, однако, приводит к
бессмысленному самоускорению зарядов (ограничиваемому лишь постулативно путем
наложения условий на величины полей). Во-вторых, само возникновение
квантовой механики говорит о том, что сила Лоренца не описывает
адекватно поведение зарядов на атомных масштабах. В-третьих, для
известного явления дрейфа частиц несколько странно, что его
скорость 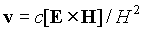 оказывается
независящей от величин заряда, массы, и самих величин полей, а
зависящей только от отношения величин полей E/H. Таким
образом, система дифференциальных уравнений современной электродинамики
и ее представлений не может рассматриваться как принципиально
строгая и полностью самосогласованная, способная налагать
ограничения на другие разделы физики. оказывается
независящей от величин заряда, массы, и самих величин полей, а
зависящей только от отношения величин полей E/H. Таким
образом, система дифференциальных уравнений современной электродинамики
и ее представлений не может рассматриваться как принципиально
строгая и полностью самосогласованная, способная налагать
ограничения на другие разделы физики.
7. Опыт Майкельсона-МорлиИзвестно, что
СТО опирается на два постулата: постулат постоянства скорости света
и принцип относительности. Итак, начнем с главного для теории
относительности вопроса: постоянна ли скорость света? Заметим, что
заранее предполагать что-либо о движении Земли было нельзя: во
времена Галилея такие опыты, например, "доказали" бы, что Земля
покоится (вообще говоря, прежде чем использовать "прибор", его надо
испытать и отградуировать в лабораторных условиях, чтобы знать, что
же он измеряет). Казалось бы ответ на вопрос о постоянстве скорости
света уже был дан в опыте Майкельсона-Морли. Однако, термин
"постоянный" означает независимость от времени, пространственных
координат, направления распространения света и, наконец, от свойств
самого света. Необходимо некоторое усилие, чтобы дать непредвзятый
ответ на вопрос: что же могло быть определено в интерферометре
Майкельсона? Отметим, что никакая скорость в опыте Майкельсона не
меряется вовсе, а измеряется разность фаз лучей (а о скорости
мы можем судить лишь косвенно). Напомним, что два световых луча
двигались во взаимно перпендикулярных направлениях. Заметим, однако,
следующее. Чтобы избежать синхронизации временных интервалов в
различных точках, оба эти световых луча двигались по замкнутым
траекториям (и в двух взаимно перпендикулярных направлениях).
Следовательно, фактически мы имеем дело в каждом из двух случаев
только со "скоростью" света, "усредненной" для взаимно
противоположных направлений. Учитывая вышесказанное, казалось бы,
результат эксперимента Майкельсона может быть сформулирован
следующим образом: средняя скорость света фиксированной частоты для двух
противоположных направлений в некоторой системе отсчета не
зависит от движения этой системы. Ни о каком глобальном постоянстве
вывода сделать нельзя. По крайней мере два вопроса все равно
остались бы в связи с локальным результатом опыта Майкельсона-Морли:
зависит или нет скорость света от пространственных координат и
времени, и зависит ли скорость света в вакууме от характеристик
самого света?
Результат опыта может быть проанализирован как с точки зрения
наличия пустого пространства (современные взгляды), так и с точки
зрения наличия эфира (причем разных взглядов на его свойства).
Известно, что свет проявляет себя в разных явлениях либо как
частица, либо как волна. Вначале предположим корпускулярную природу
света. Тогда корпускулярная модель интерферометра Майкельсона-Морли
может быть представлена в виде двух плеч с одним идеальным
отражателем в центре установки и двумя отражателями на концах плеч.
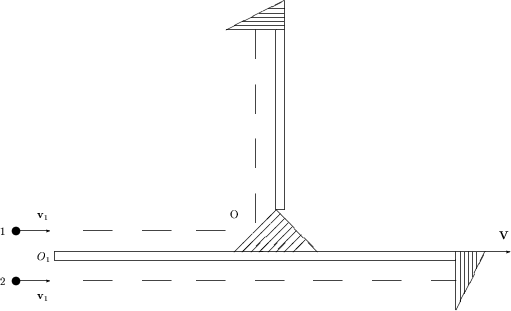
Пусть две частицы, движущиеся параллельно друг
другу со скоростью v1 (относительно
"мировой системы отсчета"), попадают в данную установку, которая
сама движется со скоростью V (относительно той же
самой системы), при этом v1 > V.
Тогда в точке O1 скорость частиц относительно
установки будет v1-V.
После отражения в центре установки частица 1 будет двигаться в
перпендикулярном направлении с той же самой (по модулю) скоростью v1-V относительно
установки. Частицы отразятся от концов плеч одновременно. Так же они
достигнут одновременно как точки O, так и точки O1.
Никакой разности скоростей этих двух частиц для двух взаимно
перпендикулярных направлений не будет наблюдаться, независимо от
скоростей v1, V.
Таким образом, если считать свет потоком частиц, то эксперименты
Майкельсона-Морли (Кеннеди-Торндайка, Томашека, Бонч-Бруевича и
Молчанова и другие) не могли дать никакого положительного
результата.
Предположим теперь волновую природу света. В этом случае скорость
света может зависеть только от свойств среды (или вакуума) и/или
внутренних характеристик самого распространяющегося света (и, также
как для звука, не зависит от скорости источника, но складывается со
скоростью приемника). Если свет представляет собой волну, то
скорость источника изменяет только частоту. Таким образом, для
данной частоты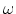 скорость
света скорость
света 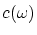 не
зависит от скорости источника. Здесь имеется в виду следующее:
световые волны одной частоты тождественны друг другу; и если мы
воспринимаем свет частоты не
зависит от скорости источника. Здесь имеется в виду следующее:
световые волны одной частоты тождественны друг другу; и если мы
воспринимаем свет частоты 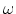 ,
то совершенно безразлично, излучался ли он источником сразу с этой
самой частотой или же излучался с частотой ,
то совершенно безразлично, излучался ли он источником сразу с этой
самой частотой или же излучался с частотой 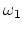 ,
но вследствие движения источника частота изменилась ,
но вследствие движения источника частота изменилась 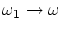 (эффект
Допплера). В обоих случаях измеряемая величина (эффект
Допплера). В обоих случаях измеряемая величина 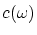 будет
одной и той же. Вернемся теперь к опытам Майкельсона-Морли и другим.
Поскольку падающий свет, свет, прошедший тонкую пластину, и свет,
отраженный от зеркал, имеют в одной и той же системе наблюдения одну
и ту же частоту, то скорость света будет
одной и той же. Вернемся теперь к опытам Майкельсона-Морли и другим.
Поскольку падающий свет, свет, прошедший тонкую пластину, и свет,
отраженный от зеркал, имеют в одной и той же системе наблюдения одну
и ту же частоту, то скорость света 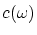 оставалась
постоянной для двух перпендикулярных направлений и эксперименты
ничего не могли обнаружить. Таким образом, попытка искать изменения
скорости света при экспериментах с одной фиксированной частотой
неверна по своей сути. Единственная зависимость, которую можно
пытаться обнаружить, есть оставалась
постоянной для двух перпендикулярных направлений и эксперименты
ничего не могли обнаружить. Таким образом, попытка искать изменения
скорости света при экспериментах с одной фиксированной частотой
неверна по своей сути. Единственная зависимость, которую можно
пытаться обнаружить, есть 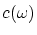 :
все другие зависимости могут войти только опосредствованно, через
эффект Допплера. :
все другие зависимости могут войти только опосредствованно, через
эффект Допплера.
Если принять гипотезу о существовании эфира, то скорость света
зависит от свойств этой среды (по аналогии со звуком). Тогда
очевидно, что скорость света не может складываться со скоростью
движения источника (гул от сверхзвукового самолета распространяется
с постоянной скоростью, фиксируемой средой и, в результате, самолет
опережает звук). Также очевидно, что поскольку свет взаимодействует
как с веществом (рассеивается или поглощается), так и с эфиром
(распространяется в нем), то должно наблюдаться и взаимодействие
эфира с веществом. А в релятивистской интерпретации опыта
Майкельсона-Морли предполагалось невероятное: жесткая "привязка"
света к эфиру вместе с полным отсутствием взаимодействия эфира с
телами (без увлечения Землей, установкой). Представьте себе, что у
кого-то возникла бы "теория", что из-за вращения Земли вокруг своей
оси должен наблюдаться постоянный ветер вдоль параллелей порядка 400
м/с. Начали его измерять флюгерами с вертушками и выяснилось, что
ветер постоянно меняется как по направлению, так и по величине в
огромных пределах в зависимости от времени и места. Из этого сделали
бы "вывод", что на Земле вовсе нет атмосферы. Естественно, в случае
частичного увлечения эфира (а для ряда локальных опытов в узком
погранслое увлечение может быть практически полным) теория
усложняется. Однако это никак не опровергает гипотезу эфира. Еще
одно замечание, касающееся эфирной интерпретации опытов.
Справедливости ради надо отметить, что опыт Майкельсона и его
аналоги (несмотря на споры по устройству прибора и теории) всегда
уверенно с учетом возможных ошибок давал ненулевой результат. Только
при экранировании металлическим кожухом результат оказывался близким
к нулевому. Для объективности вспомним, что в настоящее время все
приборы вакуумируют (делают локально закрытой системой). А,
например, локальная скорость звука в салоне самолета останется
постоянной (не зависящей от наружного ветра) даже при сверхзвуковом
движении самолета. Одна из наиболее известных эфирных точек зрения
не противоречит полученным результатам: увлечение Френеля для
металлических тел - полное (для металлов верна электродинамика
Герца), а значит эфир покоится относительно прибора (локально)
внутри металлического кожуха и искать эфирный ветер внутри -
бессмысленно. Еще один момент обычно замалчивается релятивистами.
Даже в отсутствие металлической экранировки, достаточно тончайшей
пластинки стекла (или воздуха в первоначальных экспериментах), чтобы
нужно было учитывать переизлучение света этими локально покоящимися
элементами. В результате реально наблюдаемая скорость в эфирной
концепции должна быть заведомо меньше скорости движения Земли по
орбите. Однако существует более серьезное возражение к интерпретации
экспериментов Майкельсона, так как с эфирной точки зрения анализ
стоит начать с использованных Майкельсоном формул: при их выводе
вовсе (!) не учитывалась волновая природа света, в частности эффекты
Допплера и аберрации (что можно было бы смоделировать для опытов со
звуком в воздухе). Вывод оказывается следующим: схемы с фиксированным
положением источника и приемника относительно фиксированной установки,
движущейся как целое в среде, не способны обнаружить изменение
интерференционной картины (синфазного наложения волн) при изменении
ориентации (повороте) установки (та же ситуация будет не только для
света, но и в акустике!).
Таким образом, опыт Майкельсона - Морли не свидетельствует в пользу
постоянства скорости света и не опровергает какие-либо классические
принципы.
8. Опыт Айвса-Стилуэлла и эффект Допплера для сферических
волнЗаметим, что сам Айвс был противником СТО
и объяснял опыт с позиций эфира (для СТО характерно "валить" все в
свою "кучу", чтобы "солиднее" выглядеть, делая вид, что если СТО
"потонет", то и "вся наука потонет"). Вообще говоря, в отличие от
элементарной теории эффекта Допплера для плоскопараллельных волн,
определение частотной зависимости в произвольной конфигурации -
прерогатива опыта (и не стоит приплетать сюда дополнительную
гипотезу о времени). Фактически, опыты Айвса-Стилуэла даже в идеале
(если пренебречь реальными особенностями процесса) определяли бы не
поперечный эффект Допплера, а эффект Допплера для двух направлений,
близких к 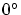 и и 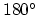 ,
то есть эффекты, близкие к продольным. Эти опыты являются
косвенными, так как величина (якобы релятивистской) поправки -
вычисляемая величина (кроме того, сравниваемая от разных областей,
что приводит к дополнительной асимметрии). Повторные опыты показали
существенные систематические отклонения от релятивистского выражения
(до 60 ,
то есть эффекты, близкие к продольным. Эти опыты являются
косвенными, так как величина (якобы релятивистской) поправки -
вычисляемая величина (кроме того, сравниваемая от разных областей,
что приводит к дополнительной асимметрии). Повторные опыты показали
существенные систематические отклонения от релятивистского выражения
(до 60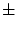 10%).
Следовательно, эффект может определяться не столько Допплеровским
выражением, сколько особенностью реакций в пучках. Дадим некоторую
критику релятивистской интерпретации рассматриваемого эксперимента.
Релятивисты описывают эксперимент так, будто поперечный эффект
Допплера воспринимается от одной точки установки в определенный
момент времени (момент пролета серединного перпендикуляра). На самом
деле воспринимаемый сигнал - это интегральная сумма от разных
областей излучения за разное время, да еще и не перпендикулярных
движению (куда, например, делась аберрация?), то есть изучаемый
эффект представляет собой некоторое "сложное среднее" между двумя
продольными эффектами Допплера. Кроме того, теория в СТО (и формулы)
приводятся для плоскопараллельных волн, а фактически на этих
расстояниях мы имеем точечные источники, т.е. сферические волны.
Рассмотрим конечный импульсный сигнал. Выпишем длины сторон в
треугольнике: 1) первая сторона изображает путь сигнала вдоль оси Y
от источника до начала координат O, где находился приемник в момент
испускания сигнала Y0=ct; 2) вторая сторона
изображает путь, пройденный приемником вдоль оси X от момента
испускания до момента получения сигнала X1=vt';
3) третья сторона (диагональ) изображает путь сигнала от источника
до точки приема ct'. Тогда из соотношения сторон треугольника можно
найти время задержки по сравнению с покоящимся случаем: 10%).
Следовательно, эффект может определяться не столько Допплеровским
выражением, сколько особенностью реакций в пучках. Дадим некоторую
критику релятивистской интерпретации рассматриваемого эксперимента.
Релятивисты описывают эксперимент так, будто поперечный эффект
Допплера воспринимается от одной точки установки в определенный
момент времени (момент пролета серединного перпендикуляра). На самом
деле воспринимаемый сигнал - это интегральная сумма от разных
областей излучения за разное время, да еще и не перпендикулярных
движению (куда, например, делась аберрация?), то есть изучаемый
эффект представляет собой некоторое "сложное среднее" между двумя
продольными эффектами Допплера. Кроме того, теория в СТО (и формулы)
приводятся для плоскопараллельных волн, а фактически на этих
расстояниях мы имеем точечные источники, т.е. сферические волны.
Рассмотрим конечный импульсный сигнал. Выпишем длины сторон в
треугольнике: 1) первая сторона изображает путь сигнала вдоль оси Y
от источника до начала координат O, где находился приемник в момент
испускания сигнала Y0=ct; 2) вторая сторона
изображает путь, пройденный приемником вдоль оси X от момента
испускания до момента получения сигнала X1=vt';
3) третья сторона (диагональ) изображает путь сигнала от источника
до точки приема ct'. Тогда из соотношения сторон треугольника можно
найти время задержки по сравнению с покоящимся случаем: 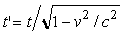 .
(По-сути, изменение времени приема сигнала может быть
интерпретировано как поперечный эффект Допплера для сферических
волн, который существует и для света и в акустике!) В результате для
реального источника будет наблюдаться смещение в красную область
(больше время действия такой смещенной частоты) и эффект может
зависеть от расстояния до точки наблюдения. Да и кто сказал, что для
света должен наблюдаться классический эффект Допплера для
плоскопараллельных волн? Ведь эффект имеет классический вид только в
случае чисто волнового движения. Если же свет - это не совсем волна,
то можно получить иные выражения, в том числе и релятивистские.
Таким образом, данный опыт не может быть вовсе отнесен к опытам,
подтверждающим релятивистское замедление времени в СТО. .
(По-сути, изменение времени приема сигнала может быть
интерпретировано как поперечный эффект Допплера для сферических
волн, который существует и для света и в акустике!) В результате для
реального источника будет наблюдаться смещение в красную область
(больше время действия такой смещенной частоты) и эффект может
зависеть от расстояния до точки наблюдения. Да и кто сказал, что для
света должен наблюдаться классический эффект Допплера для
плоскопараллельных волн? Ведь эффект имеет классический вид только в
случае чисто волнового движения. Если же свет - это не совсем волна,
то можно получить иные выражения, в том числе и релятивистские.
Таким образом, данный опыт не может быть вовсе отнесен к опытам,
подтверждающим релятивистское замедление времени в СТО.
Релятивисты для эффекта Допплера в СТО совершают очередной подлог:
они рассматривают точечные световые вспышки (то есть сферические
волны!), но результаты сравнивают с классическим эффектом Допплера
для плоскопараллельных волн. Очевидно, что для
плоскопараллельных волн никакого поперечного эффекта Доплера не
существует (и не стоит релятивистам надувать здесь щёки). Но если
кто-то не понимает разницы между сферическими и плоскопараллельными
волнами, то, по-видимому, он не понимает ни физики, ни математики
(например, на уровне 8 класса советской средней школы можно строго
найти точное решение следующей задачи: колеблющийся
вверх-вниз поплавок возбуждает круговые волны на воде; какое
количество максимумов волн в единицу времени будет фиксировать
наблюдатель, движущийся по некоторой линии над поверхностью воды?).
Рассмотрим вначале сферические волны, возбуждаемые движущимся
точечным источником в среде (например, это может быть звук
или круги на воде). Пусть покоящийся приемник сигналов находится в
точке R. Если бы источник все время покоился в точке O, то
направление распространения сигналов изобразилось бы линией OR
(длину волны можно определить, разделив расстояние |OR| на число
совершенных колебаний за время прохождения данного расстояния).
Аналогичная ситуация была бы для источника, покоящегося в некоторой
другой точке i. Пусть теперь источник движется прямолинейно с
постоянной скоростью v. Выберем условно в качестве
исследуемого сигнала участок длиной равной длине волны и
договоримся, что будем следить за точкой, соответствующей началу
этого сигнала (для равномерного движения совершенно равнозначно
можно бало бы следить за движением средины или конца этого условно
выделенного участка). В момент началаотправки сигнала
источник находился в точке O, а в момент начала приема этого
же сигнала приемником источник находится в точке i. Угол 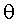 как
обычно в теории эффекта Допплера – “угол между скоростью и линией
наблюдения, измеренный в системе приемника”. как
обычно в теории эффекта Допплера – “угол между скоростью и линией
наблюдения, измеренный в системе приемника”.
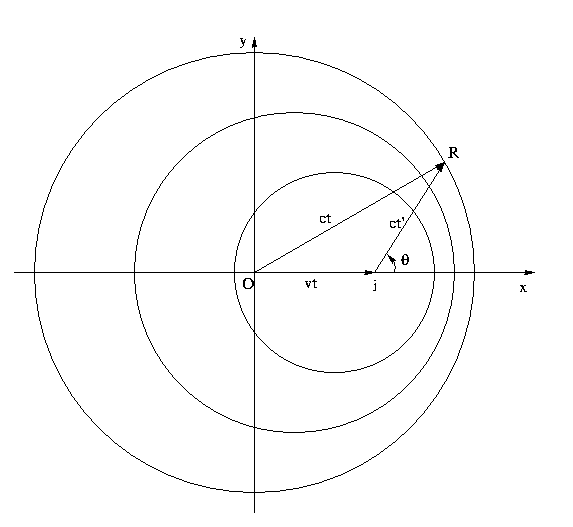
Из взаимосвязи сторон треугольника (расстояний,
или, длин волн - если длину каждой стороны разделить на число N
совершенных за это время колебаний) легко определить изменение
периода воспринимаемых колебаний T' по сравнению с периодом T
колебаний покоящегося в точке O источника (где T=t\N, T'=t'\N). Для
этого воспользуемся теоремой косинусов: 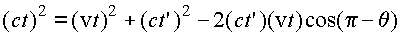 .
Решая это квадратное уравнение относительно t', имеем .
Решая это квадратное уравнение относительно t', имеем 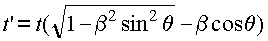 ,
где как обычно ,
где как обычно 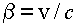 .
В итоге для изменения частоты получаем следующее выражение: .
В итоге для изменения частоты получаем следующее выражение: 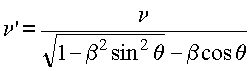 . .
Пусть теперь сферические волны возбуждаются в среде покоящимся
источником i, а приемник движется прямолинейно с
постоянной скоростью v и в момент начала приема
сигнала находится в точке R. Ситуация к этому моменту изображена на
рисунке:
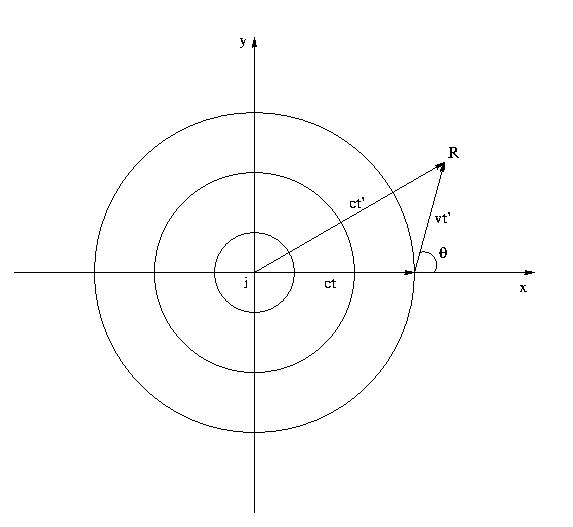
Аналогично, воспользовавшись для данного
треугольника теоремой косинусов 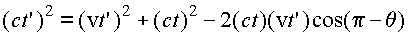 и
разрешив квадратное уравнение относительно t', найдем: и
разрешив квадратное уравнение относительно t', найдем: 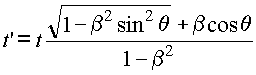 .
В итоге формула эффекта Допплера для сферических волн будет иметь
вид: .
В итоге формула эффекта Допплера для сферических волн будет иметь
вид: 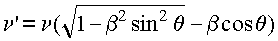 .
Из самой процедуры получения формулы следует ее верность при любых
расстояниях. Фактически угол .
Из самой процедуры получения формулы следует ее верность при любых
расстояниях. Фактически угол 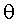 и
отслеживает автоматически расстояние между источником и приемником,
так как, в отличие от случая плоскопараллельных волн, этот угол
меняется в процессе движения. В полученной формуле нас прежде всего
интересует тот факт, что для сферических волн существует поперечный
эффект Допплера (если подставить в последнюю формулу эффекта
Допплера и
отслеживает автоматически расстояние между источником и приемником,
так как, в отличие от случая плоскопараллельных волн, этот угол
меняется в процессе движения. В полученной формуле нас прежде всего
интересует тот факт, что для сферических волн существует поперечный
эффект Допплера (если подставить в последнюю формулу эффекта
Допплера 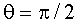 ),
полностью совпадающий с релятивистским выражением. При одновременном
движении источника и приемника эффект Допплера для сферических волн
имеет вид: ),
полностью совпадающий с релятивистским выражением. При одновременном
движении источника и приемника эффект Допплера для сферических волн
имеет вид: 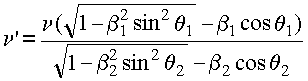 .
Теперь вернемся к "нашим релятивистам". Последним из релятивистов,
кто записывал одну релятивистскую формулу одновременно включающую и
движение источника и движение приемника, был Макс Лауэ. Потом,
видать, релятивисты поняли притиворечие одновременного учета обоих движений
самой идеологии релятивизма, но не договорились какую же из двух
формул оставить (ведь у А.Эйнштейна их две!). В результате в
литературе у разных авторов встречаются разные формулы. Кроме того
непонятно, как одна релятивистская формула эффекта Допплера
могла бы при предельном переходе одновременно дать две классические
формулы эффекта Допплера (ведь, например, для звука обе они
экспериментально проверены и дают разные наблюдаемые результаты)? .
Теперь вернемся к "нашим релятивистам". Последним из релятивистов,
кто записывал одну релятивистскую формулу одновременно включающую и
движение источника и движение приемника, был Макс Лауэ. Потом,
видать, релятивисты поняли притиворечие одновременного учета обоих движений
самой идеологии релятивизма, но не договорились какую же из двух
формул оставить (ведь у А.Эйнштейна их две!). В результате в
литературе у разных авторов встречаются разные формулы. Кроме того
непонятно, как одна релятивистская формула эффекта Допплера
могла бы при предельном переходе одновременно дать две классические
формулы эффекта Допплера (ведь, например, для звука обе они
экспериментально проверены и дают разные наблюдаемые результаты)?
9. ОТО - "великая" теория трех с половиной наблюдений
Обычно, даже если есть сотня разных данных, не всегда строится
теория - данные проще свести в таблицу. В случае же с ОТО мы имеем
"Великую теорию трех с половиной наблюдений", из которых три -
фикция. По поводу отклонения света в гравитационном поле от
прямолинейного движения надо сказать следующее. Во-первых, как
отмечало большинство экспериментаторов, количественное подтверждение
эффекта существенно зависит от веры конкретного экспериментатора.
Во-вторых, уже из классической формулы 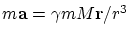 следует,
что любой объект, даже нулевой массы, будет падать в гравитационном
поле. В-третьих, с чем, собственно, сравнивается эффект? С абсолютно
пустым пространством? Еще в 1962 году группа Королевских астрономов
заявила, что отклонение луча света вблизи Солнца не может
рассматриваться как подтверждение ОТО, так как у Солнца существует
атмосфера, простирающаяся на огромное расстояние. Напомним, что
явление рефракции учитывается для земной атмосферы астрономами уже
очень давно. Еще Ломоносов обнаружил отклонение луча света в
атмосфере Венеры. Для пояснения, представьте себе стеклянную сферу.
Естественно, что параллельные лучи (от далеких звезд) будут
отклоняться в ней к центру. Такая система всем знакома как
оптическая линза. Подобная ситуация будет и для газовой сферы
(атмосферы Солнца). Для точного расчета отклонения луча света в
гравитационном поле нужно учесть наличие атмосферы Солнца и то, что
наличие градиентов плотности и температуры на пути луча вызывает
изменение показателя преломления среды и, следовательно, искривление
луча света. И уж если на расстоянии сотни метров вблизи земной
поверхности эти эффекты вызывают мираж, то не учитывать их для луча
от звезды, проходящего вблизи Солнца миллионы километров - это
чистая спекуляция. следует,
что любой объект, даже нулевой массы, будет падать в гравитационном
поле. В-третьих, с чем, собственно, сравнивается эффект? С абсолютно
пустым пространством? Еще в 1962 году группа Королевских астрономов
заявила, что отклонение луча света вблизи Солнца не может
рассматриваться как подтверждение ОТО, так как у Солнца существует
атмосфера, простирающаяся на огромное расстояние. Напомним, что
явление рефракции учитывается для земной атмосферы астрономами уже
очень давно. Еще Ломоносов обнаружил отклонение луча света в
атмосфере Венеры. Для пояснения, представьте себе стеклянную сферу.
Естественно, что параллельные лучи (от далеких звезд) будут
отклоняться в ней к центру. Такая система всем знакома как
оптическая линза. Подобная ситуация будет и для газовой сферы
(атмосферы Солнца). Для точного расчета отклонения луча света в
гравитационном поле нужно учесть наличие атмосферы Солнца и то, что
наличие градиентов плотности и температуры на пути луча вызывает
изменение показателя преломления среды и, следовательно, искривление
луча света. И уж если на расстоянии сотни метров вблизи земной
поверхности эти эффекты вызывают мираж, то не учитывать их для луча
от звезды, проходящего вблизи Солнца миллионы километров - это
чистая спекуляция.
Смещение перигелия Меркурия - эффект, конечно, красивый (но в
единственном экземпляре - не мало ли для "привлечения научной
теории"). Солнце не является твердым телом и движение Меркурия может
вызывать на Солнце приливную волну, которая может в свою очередь
влиять на смещение перигелия Меркурия. В любом случае необходимо
знать скорость передачи гравитационных взаимодействий для вычисления
влияния прилива от Меркурия и других планет на характеристики орбиты
Меркурия, чтобы можно было отделить чисто "гравитационный" эффект
общей теории относительности (если бы этот "чистый" эффект вообще
существовал). При расчете в ОТО смещения перигелия (из строгого
решения для единственной притягивающей точки) создается впечатление,
что мы знаем точные массы астрономических тел. На самом деле, если
мы пользуемся ОТО как поправкой к теории Ньютона, то ситуация
противоположная: стоит задача по видимому движению планет
восстановить их точные массы, чтобы потом подставить их для проверки
ОТО. Представим себе, что орбита планеты - круговая. В этом случае
сразу очевидно, что период вращения в теории Ньютона уже будет взят
с учетом невидимой прецессии, то есть перенормирован. Поэтому в
теорию Ньютона уже входят некоторым образом (усредненно)
перенормированные массы. Поскольку поправки ОТО во много раз меньше
возмущающего влияния всех планет и влияния несферичности,
восстановление точных масс в этой сложной задаче многих тел может
существенно изменить описание всей картины движения, что нигде не
учтено. Вообще говоря, ситуация с описанием смещения перигелия
Меркурия типична для поведения релятивистов. Во-первых, объявляется,
что эффект был предсказан, хотя Эйнштейн сравнивал его с известными
результатами приближенных расчетов Лапласа, полученными задолго до
ОТО. Надеюсь, каждый человек понимает огромную разницу между
"предсказать" и "объяснить задним числом" (вспомним анекдот от
Фейнмана). Во-вторых, прецессия была и в классической физике: по
данным 19 века итоговая величина прецессии за счет влияния некоторых
других планет расчитывалась как 588'', а недостающая расчетная
величина была всего около 43'', то есть составляла малую поправку.
(Заметим, что по некоторым данным 20 века указывается общая величина
прецессии почти на порядок большая, но при этом сохраняется из ОТО
величина в 43'' - "табу"; впрочем, это может быть и опечатка - не
будем придираться по мелочам к 1/3 от "огромной экспериментальной
базы ОТО"). В-третьих, точный расчет в задаче многих тел даже
современная математика пока выполнить не в состоянии. В классическом
случае расчет проводился как сумма независимых поправок от влияния
отдельных планет (и Солнце и планеты считались материальными
точками). Естественно, в классическом случае итоговый результат (уже
более 90 процентов от наблюдаемого!) может быть еще улучшен при
учете несферичности Солнца, влияния всех планет (и малых тел)
Солнечной системы и того факта, что Солнце - не твердый объект
(материальная точка) и его локальная плотность в разных слоях просто
обязана "отслеживать" влияние остальных движущихся планет (на этом
пути привлечения более реальных конкретных физических механизмов
вполне может получиться недостающий малый эффект). Но то, что
декларируют релятивисты - уму непостижимая спекуляция! Они "находят"
эффект (причем только этот малый процент!), рассмотрев движения лишь
двух материальных точек - Солнца и Меркурия. Простите, а как Ваша
ОТО подкорректирует уже найденную из классики большую часть эффекта?
Боитесь считать? Тогда о каком "блестящем совпадении" вы твердите?
Чистая подгонка под желаемое!
Напомним теперь два известных опыта, срочно отнесенных релятивистами
в пользу ОТО. В опыте Хефеля-Киттинга две пары цезиевых часов
путешествовали на самолетах в западном и восточном направлениях и их
показания сравнивались с покоившимися часами (при этом учитывалась
"скоростная добавка" СТО, а выше доказано ее отсутствие). В опыте
Паунда и Ребки с помощью эффекта Мессбауэра определялся сдвиг частот
фотона при прохождении им некоторого пути в вертикальном направлении
как вверх, так и вниз. В физике не принято дважды учитывать одно и
тоже влияние. Ясно, что ускорение и гравитация выражают некоторую
силу, влияющую на разные процессы. Но это будет общий результат
действия именно сил. Например, не всякую перегрузку выдерживает
человек, маятниковые настенные часы в невесомости идти не будут, но
это не означает, что время остановилось. Поэтому грубый опыт
Хефеля-Киттинга констатирует тривиальный факт, что гравитация и
ускорение каким-то образом влияют на процессы в цезиевых атомных
часах и высокая относительная точность этих часов для фиксированного
места совершенно ни при чем. Хотя опыт Хефеля-Китинга и объявлен как
подтверждающий ОТО, этот вывод был получен на основе малой
(урезанной) выборки. Другие исследователи, получившие доступ к тем
же первичным данным сделали прямо противоположный вывод. При этом
опыт Хефеля-Киттинга был истолкован в пользу зависимости времени от
гравитации (интерпретация фактически означает изменение самой
несущей частоты генератора в гравитационном поле). Однако, в таком
случае он противоречит интерпретации опыта Паунда-Ребки, где
считалось, что генератор дает одну и ту же частоту на любой высоте
(и какой-то из опытов нужно исключать из "копилки" теории
относительности). Гравитационное смещение истолковывалось с
энергетических позиций и в классической физике, но куда же тогда
девать якобы существующее замедление времени в поле тяжести?
Многие трудности ОТО общеизвестны: 1) нарушен принцип соответствия
(без введения искусственных внешних условий не существует
предельного перехода к случаю без гравитации); 2) отсутствуют законы
сохранения; 3) относительность ускорений противоречит
экспериментальным фактам (вращающиеся жидкости в космосе имеют форму
эллипсоидов, в то время как невращающиеся - шара); 4) существуют
сингулярные решения. (Обычно, любая теория считается в подобных
случаях неприменимой, но теория относительности для сохранения
своего "всеобщего характера" начинает строить фантастические образы:
черных дыр, Большого взрыва и т.д..) Вам выбирать, стоит ли
заниматься подобным "литературным творчеством", по крайней мере, к
науке эта "поэзия" точно не имеет отношения.
10. Почему же все-таки Ньютон?
(апологетика классической физики)Классические
понятия физики оформились как обобщение тысячелетних наблюдений
добросовестных исследователей над окружающим миром (включая
астрономические наблюдения Вселенной). Если одной из целей науки
считать определение причинно-следственных связей явлений, то важный
позитивный момент классического подхода заключается в отделении
объекта исследования от остальной Вселенной. Например, в подавляющем
большинстве случаев движение глаз наблюдателя не оказывает заметного
влияния на конкретный протекающий процесс, и уж тем более на всю
оставшуюся Вселенную. Конечно, бывают "кажущиеся эффекты", но от них
обычно избавляются градуировкой приборов, пересчетом и т.д., чтобы
сосредоточиться именно на исследуемом процессе. Классические понятия
кинематики фактически и были введены Ньютоном для определения
независимых от исследуемого процесса реперных точек и эталонов. Это
создает базу для единого описания самых различных феноменов,
стыковки разных областей знания и упрощения описания. Ньютон,
исходивший из практических потребностей естествознания, осознавал,
что такими базовыми понятиями, как пространство и время, прекрасно
"владеют и практически пользуются" любые живые существа, например,
насекомые (неспособные по мнению людей к абстрактному мышлению).
Следовательно, эти понятия относятся к основным, то есть
неопределяемым через что-либо понятиям. Значит, можно дать только
перечисление того, что будет подразумеваться под этими понятиями или
использоваться на практике, и выделить ту абстракцию, которая будет
подразумеваться в идеализированных математических выкладках. Поэтому
Ньютон четко отделил абсолютное, истинное, математическое время или
длительность (в данном случае это просто синонимы!) от
относительного, кажущегося или обыденного времени. Таким образом,
время означает математическое сопоставление длительности
исследуемого процесса с длительностью эталонного процесса.
Возможность введения единого времени в классической физике напрямую
не была связана с очевидной конечной скоростью передачи сигналов.
Скорее получение единого времени связано с уверенностью в
возможность пересчета времени с заданной практической точностью из
местного (локального) времени. Совершенно аналогичным образом Ньютон
отделил абсолютное пространство от относительного, выделил
абсолютное и относительное место и разделил абсолютное и
относительное движение. Как показало развитие науки, классические
представления кинематики не приводят к внутренним логическим
противоречиям или к противоречиям с экспериментами. Да и интуитивно
классические понятия совпадают с тем, что дано нам в ощущениях и не
пользоваться этим - все равно, что силиться ходить на ушах.
Имеет ли смысл обсуждать так называемые кинематические эффекты
(например, мифическое искривление пространства)? Разумеется нет:
если считать само пространство искривляющимся, то точно так же
искривлялись бы и линейки и подобное искривление никак не могло бы
быть обнаружено. Именно поэтому классические понятия выбраны
идеальными (и наиболее простыми в практическом использовании).
Мешают ли классические понятия "наполнению" реальной материи
какими-либо свойствами? Не мешают вовсе! Любое свойство материи,
которое открыто или может быть открыто в будущем легко и органично
будет включено в классическую физику. Например, в классической
физике вполне адекватным является обсуждение возможных свойств эфира
(а в СТО нет никакого смысла обсуждать эфир, поскольку в СТО он
лишен наблюдаемых свойств). В классической физике вполне могут
обсуждаться вопросы генерации массы, заряда и т.д. Мешает ли
классическая физика потенциальной возможности существования
многоуровневых систем и движений (до бесконечности вглубь и вширь и
столь же разнообразных)? Тоже не мешает. Первый "закон" Ньютона
говорит лишь об идеальном прямолинейном движении выделенного тела,
не взаимодействующего ни с каким другим объектом. В реальной же
Вселенной такая ситуация строго не проявляется (а лишь иногда и
приближенно). Поэтому какой тип естественного движения (например,
движение по окружности или другие) реализуется в нашей единственной
Вселенной целиком определяется существующими реальными
взаимодействиями.
Теперь о втором законе Ньютона. Взаимодействие тел приводит к
изменениям в состоянии тел. Необходимо выбрать индикатор этого
изменения. Ньютон выбрал наблюдать за ускорением тела в качестве индикатора изменения
его состояния движения. По-сути, второй закон Ньютона представляет
собой определение понятия "сила" и с точки зрения функциональной
зависимости сила и ускорение совпадают с точностью до размерного
коэффициента (массы). В идеале, этот способ описания движения (в
привычном нам виде) записывается как ma=F(t,r,v).
Релятивистское уравнение движения с силой 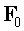 элементарно
может быть записано как второй закон Ньютона (см. выше) с силой элементарно
может быть записано как второй закон Ньютона (см. выше) с силой 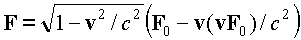 .
Хотя природа и не всегда с легкостью раскрывает нам свои секреты, но
можно быть уверенным, что принцип второго закона Ньютона останется
верным: вместо идеального выражения силы всегда можно
воспользоваться тем, что найдем из опыта: .
Хотя природа и не всегда с легкостью раскрывает нам свои секреты, но
можно быть уверенным, что принцип второго закона Ньютона останется
верным: вместо идеального выражения силы всегда можно
воспользоваться тем, что найдем из опыта: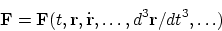 .
Из этого обобщенного выражения видно, что любая производная (в том
числе и вторая) ничем не выделена и только эксперимент может
определить разновидности сил, реализующихся в природе (например,
вспомним предложенную Вебером задолго до СТО формулу, где сила
зависела от ускорения). Будет ли для описания движения найдена более
"экономная" запись, чем второй закон Ньютона, покажет будущее (такое
"улучшение", вообще говоря, возможно, но это не вопрос о верности
или неверности самого принципа описания!). Уравнения движения
полностью (!) определяют интегралы движения и это вовсе не обязаны
быть классические механические энергия и импульс, введенные для
невзаимодействующих бесструктурных материальных точек (вспомним про
классические же примеры с реальными диссипативными процессами, про
гидродинамические примеры и т.д.). .
Из этого обобщенного выражения видно, что любая производная (в том
числе и вторая) ничем не выделена и только эксперимент может
определить разновидности сил, реализующихся в природе (например,
вспомним предложенную Вебером задолго до СТО формулу, где сила
зависела от ускорения). Будет ли для описания движения найдена более
"экономная" запись, чем второй закон Ньютона, покажет будущее (такое
"улучшение", вообще говоря, возможно, но это не вопрос о верности
или неверности самого принципа описания!). Уравнения движения
полностью (!) определяют интегралы движения и это вовсе не обязаны
быть классические механические энергия и импульс, введенные для
невзаимодействующих бесструктурных материальных точек (вспомним про
классические же примеры с реальными диссипативными процессами, про
гидродинамические примеры и т.д.).
В классической физике присутствуют не только относительные величины,
но и абсолютные величины (и это прекрасно работает на практике),
значит она уже является более общей теорией, чем любая теория, не
содержащая абсолютных величин.
Еще пара замечаний мелким шрифтом.
О воровстве (плагиате идей). Эту тему обсуждают многие авторы.
Воровская "логика" (апологетика) релятивистов гласит: "обвинение
А.Эйнштейна в воровстве чужих интересных идей противоречит
утверждению об ошибочности теории относительности". Отнюдь нет: если
кто-то украл автомобиль, а затем его разбил, то факт отсутствия
работающего автомобиля не отменяет факт его первоначального
воровства. Например, идеи теории относительности содержатся в более
ранних работах А.Пуанкаре, формулы СТО имеются в более ранних
работах Х.Лоренца (а ссылок ни на одного ! из своих многочисленных
предшественников А.Эйнштейн не дал).
Однако различие в интерпретациях формул является достаточно
существенным. Например, если Очень Большой Релятивистский Ученый
скажет, что он сжал всю Вселенную, когда шел в соседнюю булочную, то
куча "подпевал" подтвердят эту чушь (видать эти бедняги не читали в
детстве сказку "Голый король"). А ведь для данного так называемого
"кинематического эффекта" нет ни причины, ни механизма его
реализации (действия): с чего это вся Вселеная сжалась, если идти
взбрело в голову только одному человеку (даже если он "пуп земли")?
Следовательно, подобному эффекту нет места в физике (это лишь
математический трюк). У Лоренца, напротив, не каждый объект сжимался
относительно каждого при взаимном движении (и уж тем более не все
пространство), а только тот, кто конкретно двигался сквозь эфир.
Здесь присутствует и причина (начало движения с конкретной скоростью
сквозь эфир) и механизм (взаимодействие с эфиром). Такой эффект уже
вполне может обсуждаться в физике. В интерпретациях формул и состоит
отличие физики от математики.
Еще раз напомним, что данный раздел дает лишь краткое представление
о направлениях критики теории относительности и не подменяет собой
более обоснованные полные версии работ. Так что стоит прочесть
оригиналы!
|

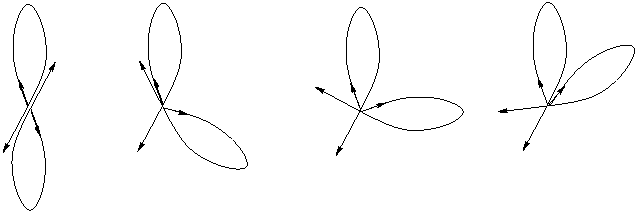





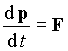 в
явном виде найти производную от релятивистского импульса, умножить
скалярно левую и правую части уравнения на v. Тогда
получается соотношение
в
явном виде найти производную от релятивистского импульса, умножить
скалярно левую и правую части уравнения на v. Тогда
получается соотношение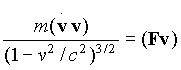 .
.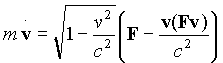 .
.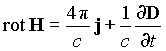 ,
, 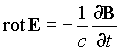 ,
,

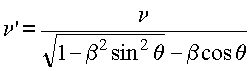 .
.
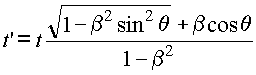 .
В итоге формула эффекта Допплера для сферических волн будет иметь
вид:
.
В итоге формула эффекта Допплера для сферических волн будет иметь
вид: 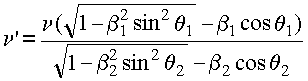 .
Теперь вернемся к "нашим релятивистам". Последним из релятивистов,
кто записывал одну релятивистскую формулу одновременно включающую и
движение источника и движение приемника, был Макс Лауэ. Потом,
видать, релятивисты поняли притиворечие одновременного учета обоих движений
самой идеологии релятивизма, но не договорились какую же из двух
формул оставить (ведь у А.Эйнштейна их две!). В результате в
литературе у разных авторов встречаются разные формулы. Кроме того
непонятно, как одна релятивистская формула эффекта Допплера
могла бы при предельном переходе одновременно дать две классические
формулы эффекта Допплера (ведь, например, для звука обе они
экспериментально проверены и дают разные наблюдаемые результаты)?
.
Теперь вернемся к "нашим релятивистам". Последним из релятивистов,
кто записывал одну релятивистскую формулу одновременно включающую и
движение источника и движение приемника, был Макс Лауэ. Потом,
видать, релятивисты поняли притиворечие одновременного учета обоих движений
самой идеологии релятивизма, но не договорились какую же из двух
формул оставить (ведь у А.Эйнштейна их две!). В результате в
литературе у разных авторов встречаются разные формулы. Кроме того
непонятно, как одна релятивистская формула эффекта Допплера
могла бы при предельном переходе одновременно дать две классические
формулы эффекта Допплера (ведь, например, для звука обе они
экспериментально проверены и дают разные наблюдаемые результаты)?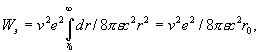 (24)
(24)