MAXIMA

Maxima

Maxima - это весьма удобный и продвинутый калькулятор для конкретных инженерных и прикладных аналитических расчетов. Начиная со школьных задач - сложные геометрические расчеты, решение квадратных и кубических уравнений, систем линейных уравнений, взятие сложных производных, решение тригонометрических и дифференциальных уравнений. Плюс построение графиков. Стильный и мощный инструмент для продвинутых школьников, студентов и любителей науки.

Maxima - это система "компьютерной алгебры" для работы с символьными и численными выражениями, включая дифференцирование, интегрирование, разложения в ряды Тейлора, преобразования Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, полиномы, множества, списки, векторы, матрицы и тензоры. axima производит численные расчеты высокой точности, используя точные дроби, целые числа и числа с плавающей точкой произвольной точности (точность вычислений в 16 значимых цифр и до 100 и больше). Maxima позволяет строить графики функций и статистических данных в двух и трех измерениях..

Maxima - универсальный свободный инструмент, сравнимый по своим возможностям с платными Mathematica, MATLAB, Maple, Derive. Среди свободных программ с ней сопоставимы Octave и SageMath, которая заимствовала часть алгоритмов из Maxima, и. Ну и "весит" Maxima 180 мб, в отличие от 32 Гб MATLAB. Я решал конкретную астрономическую задачу: попробовал Excel, надстройку xlPrecision для него, Scilab, Octave, Mathcad и лучшей - по приятности, эргономике и высокой точности расчетов оказалась wmMaxima.

Maxima для Windows - сама программа

Академия ALT Linux: Компьютерная математика с Maxima

Академия ALT Linux: Введение в Octave (альтернатива Maxima)

(wx)Maxima за 10 минут (открыть в Maxima)

wxMaxima Manual

Maxima 5.41.0 Manual

Если текст большой, то расширения-переводчики могут его не перевести. Тогда делаем гугл-поиск по названию документа и там нам предоставляется возможность перевода.

Maxima 5.41.0 Manual: - Maxima, a Computer Algebra System

maxima.sourceforge.net/docs/manual/maxima.html Перевести эту страницу

Maxima - как калькулятор
Maxima - возможности

Н.А. Стахин. Основы работы с Maxima. 2008.

Тихон Тарнавский о Maxima. 2006 год:

Приложение к 6-й статье — «Пишем свой diff()».

Практические задания по высшей математике с применением программы Maxima для студентов, обучающихся по специальности социология/ Д.Ф. Абзалилов, М.С. Малакаев,Е.А. Широкова – Казань: КФУ, 2012 г. Часть 2 - 2013 год.

Зачем Maxima школьнику и студенту? или «Задача о невесомом медведе»

Помогите разобраться в программе Maxima (хороший форум)

Системы компьютерной алгебры (интересная статья)

Темы про Maxima на Киберфоруме

Самоучители по Maple, MathCAD, Mathematica, MatLab, SPSS.

Числа e , π , φ (золотое сечение) записываются как "%e" "%pi"."%phi"
Золотое сечение можно вычислить на ходу: φ=(5^(1/2)-1)/2 ~ 0,618 034.

Десятичный разделитель "." (то есть "," здесь не пройдет).

Запись степеней десятки удобнее делать в форме "e"-мантиссы. Например,
0.1=1e-1; 0.0000025=2.5e-6; 1500000000=1.5e9=1.5*10^9

Оператор "float" используется для представления обыкновенных дробей в виде десятичных.

float(1/2+1/3); или
1/2+1/3, float;

Чтобы получить более точный расчет, выделяем нужную строку (%..) и в "Меню/Численные расчеты" выбираем "в число с плавающей точкой повышенной точности". Или используем функцию "bfloat(%on);", где n - номер строки, которую надо вычислить поточнее. Можно прямо "bfloat(1/2+1/3);" или "(1/2+1/3), bfloat".

При этом "e"-мантисса заменяется на "b"-мантиссу. Иначе результат не получим. Все числа записываем в форме b-мантиссы!

Число цифр управляется командой "fpprec: N;". По умолчанию N=16. Для увеличения числа значащих цифр команду, например, "fpprec: 100;" надо выполнить перед командой "bfloat(%on);".

Или же выполняем "fpprec: 100;" и далее все числа записываем в форме b-мантиссы.

Чтобы присвоить значение переменной, Maxima использует двоеточие (:), а не знак равенства. Знак равенства используется для представления уравнений. Благодаря переменным можно сложный расчет разбить на последовательную серию, определяя по пути константы, коэффициенты, соотношения... Другой способ - использовать в формулах предыдущие строки. Например, "5+%o32".

Maxima в Windows понимает Unicode, поэтому можете называть переменные по русски.

Запись основных операций:
• + сложение
• - вычитание
• * умножение
• / деление
• ** или ^ возведение в степень
• sin(x), cos(x)......
• abs(x) модуль x

В Maxima используется вместо tg – tan, вместо ctg – cot, вместо arcsin – asin, вместо arccos – acos, вместо arctg – atan, вместо arcctg – acot, вместо ln – log, вместо cosec – csc.

Угловая мера в Maxima – радианы. Перевод градусов в радианы x°=πx/180 радиан.
Обратно: x радиан = (x*180/π)°.

Случайное число random(N) – целое, из промежутка [0, N-1].

В контекстном меню рабочего поля можно выбрать "Вставить Заголовок/Раздел/Подраздел или Комментарий и можно добавить свои пояснения.

В комментарии можно вставлять изображения, предварительно скопировав их в буфер обмена (формат bmp). При сохранении документа изображение сохраняется внутри него в виде кода формата png.

Приближения в малых углах

cos²x = 1 - sin²x

sinx ~ x tagx ~ x cosx ~ 1-x²/2

sinx ~ x - x³/3! + x⁵/5! = x - x³/6 + x⁵/120...

cosx ~ 1 - x²/2! + x⁴/4! = 1 - x²/2 + x⁴/24...

tagx ~ x + x³/3 +2x⁵/15...

ВСЕ ПОДСКАЗКИ ДНЯ WXMAXIMA

Здесь представлены те подсказки, которые мы с вами видим при запуске wxMaxima (если не отключили их показ). Некоторые показываемые подсказки на английском языке, поэтому для ликвидации этого пробела было решено их все выписать и перевести те, которые этого требуют. Здесь собраны все доступные подсказки, но убраны те, которые однозначно потеряли актуальность.

• Чтобы сразу приступить к использованию wxMaxima, начните вводить вашу команду. Должна появиться ячейка ввода. Затем нажмите Shift-Enter для вычисления вашей команды.

• По умолчанию Shift-Enter используется для вычисления команд, а Enter используется для множественного ввода. Это поведение может быть изменено в окне 'Правка'->'Настройка' галочкой «Enter отправляет ячейку на вычисление». Тогда после нажатия Enter ячейка будет вычисляться, а Shift-Enter будет использоваться для множественного ввода.

• Maxima использует ':' для присвоения значений ('a : 3;') и ':=' для определения функций ('f(x) := x^2;').

• Самый последний результат вычисления обозначается '%'. Результат любого другого предыдущего вычисления обозначается '%on', где n – порядковый номер вычисления.

• Maxima поддерживает три типа чисел: точные дроби (они могут быть сгенерированы, например, набором 1/10), числа с плавающей точкой стандарта IEEE 754 (0.2) и big float с произвольной точностью (1b-1). Обратите внимание, что, в силу своей природы двоичных, а не десятеричных цифр, нет, например, способа сгенерировать IEEE число с плавающей точкой, в точности показывающее 0.1.. Если вместо дробей используются числа с плавающей точкой, то Maxima иногда вводит (хоть и очень маленькую) ошибку и использует 3602879701896397/36028797018963968 для 0.1 вводя (хоть и очень маленькую) ошибку.

• Если вы печатаете оператор (один из +*/^=,) в качестве первого символа в ячейке ввода, перед оператором автоматически будет вставлено %, как в графическом калькуляторе. Вы можете отключить эту функцию в окне 'Правка'->'Настройка'.

• Используя меню «Ячейка», вы можете вставить различные типы «ячеек» в документе wxMaxima. Помните, что только «ячейка ввода» может быть вычислена, а остальные используются для комментирования и структурирования ваших расчётов.

• Ячейки заголовка, раздела и подраздела могут быть свёрнуты, для сокрытия своего содержимого. Для свёртывания или развёртывания, кликните на квадратике рядом с ячейкой. Если при клике вы зажмёте клавишу shift, то все подуровни этой ячейки также будут свёрнуты/развёрнуты.
Вы можете скрыть вывод части ячеек, кликая на треугольнике с левой части ячеек. Это также работает на текстовых ячейках.

• В Интернете много ресурсов о Maxima и wxMaxima. Посетите http://andrejv.github.com/wxmaxima/help.html для дополнительной информации и для поиска инструкций по использованию wxMaxima и Maxima.

• Вы можете получить помощь по функциям Maxima выделив или кликнув имя функции и нажав F1. wxMaxima будет искать выделенный текст или текст подо курсором по индексу справки.

• В wxMaxima 0.8.0 появился горизонтальный курсор. Он выглядит как горизонтальная черта между ячейками. Он означает, что на этом месте будет создана новая ячейка, если вы введёте текст или выполните команду.

• Горизонтальный курсор работает как нормальный курсор, но воздействует на ячейки: нажмите стрелочку вверх или вниз для их перемещения, удерживаете нажатой Shift во время перемещения выбранных ячеек, нажмите дважды backspace или delete для удаления следующей за этой ячейки.
Выделение части вывода и правый клик на выделении вызовет меню с удобными функциями, применимыми для выделения.

• Вы можете выбрать несколько ячеек как с помощью мыши – нажав кнопку мыши и перемещая курсор между ячейками или по скобе ячейки слева; или с помощью клавиатуры – удерживая Shift во время движения горизонтального курсора и затем работая с выделением. Это удобно, когда вы хотите удалить или вычислить несколько ячеек.

• Вы можете вычислить весь ваш документ, используя меню команд 'Ячейка->Evaluate All Cells (вычислить все ячейки)' или соответствующую комбинацию клавиш. Ячейки будут вычислены в порядке появления в документе.

• Если ваше вычисление слишком затянулось, вы можете попробовать команды в меню 'Maxima->Прервать' или 'Maxima->Перезапустить Maxima'.

• Чтобы построить график в полярных координатах, установите 'полярные координаты' в опциях диалога 'Двумерный график'. Для трех измерений можно также выбрать сферические и цилиндрические координаты.

• Диалоги wxMaxima применяют команды со стандартными аргументами, обычно '%'. Если вы выделите текст в документе, то вместо '%' будет использован он.

• Для вставки скобок вокруг выражения, выделите его и нажмите '(' или ')' в зависимости от того, где вы хотите чтобы появился курсор.

• При применении функции с одним аргументом из меню аргументом по умолчанию выбирается '%'. Если нужно применить функцию к другому аргументу, необходимо выделить его в документе.

• Чтобы размер и положение окна wxMaxima запоминались от сессии к сессии используйте 'Правка->Настройка'

• Начиная с wxMaxima 0.8.2 вы также можете вставить в ваш документ изображения. Используйте меню команды 'Ячейка->Вставить изображение…'. Помните, что вам нужно сохранить ваш документ в формате Whole document (*.wxmx), чтобы изображения были также сохранены.

• Кроме глобальной команды Отмена, которая активна, когда курсор расположен между ячейками, wxMaxima имеет функцию Отмена в отношении каждой ячейки, функция активна, если курсор внутри ячейки. Следовательно нажатие Ctrl+Z внутри ячейки может использоваться для тонкой команды Отмена, которая не влияет на изменения, сделанные позже в других ячейках.

• Нажатие Ctrl+Space или Ctrl+Tab запускает функцию автодополнения, которая не только завершает все функции и их параметры, которые интегрированы в ядро Maxima: она также знает о параметрах из загруженных в настоящий момент пакетов и из функций, которые определены в текущем файле.

• Возможно задать многократно используемые библиотеки Maxima с wxMaxima, которые затем загружаются с использованием функции load(). Всё, что нужно сделать для этого, – это экспортировать файл в формате .mac.

• Можно настроить команды, которые будут выполняться при кажодм запуске wxMaxima, для этого поместите их в текстовый файл с именем wxmaxima.rc в пользовательской директории. Эта директория может быть найдена введя maxima_userdir.

• Независимо от того, в какой директории был запущен процесс wxMaxima, он может получить доступ к библиотекам, если они размещены в пользовательской директории. Эту директорию можно узнать набрав maxima_userdir.

Пример:

Вычислить значение производной функции $y(x)=x^2 \cdot e^{-x}x$ :

(%i1)	diff(x^2*exp(-x),x);

$2\,x\,{e}^{-x}-{x}^{2}\,{e}^{-x}\leqno{(\%o1) }$

(%i2)	f(x):=''%;

$f\left( x\right) :=2\,x\,{e}^{-x}-{x}^{2}\,{e}^{-x}\leqno{(\%o2) }$

Двойная кавычка перед символом предыдущей операции позволяет заместить этот символ значением, т.е. текстовой строкой, полученной в результате дифференцирования.

Подстановка в рациональных выражениях осуществляется функцией ratsubst . Синтаксис вызова: ratsubst(a,b,c) Выражение подставляется вместо выражения в выражении ( может быть суммой, произведением, степенью и т.п.).

Пример использования ratsubst :

(%i1)	ratsubst (a, x*y^2, x^4*y^3 + x^4*y^8);

$a\,{x}^{3}\,y+{a}^{4}\leqno{(\%o1) }$

(%i2)	cos(x)^4 + cos(x)^3 + cos(x)^2 + cos(x) + 1;

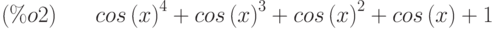
${cos\left( x\right) }^{4}+{cos\left( x\right) }^{3}+{cos\left( x\right) }^{2}+cos\left( x\right) +1\leqno{(\%o2) }$

(%i3)	ratsubst (1 –- sin(x)^2, cos(x)^2, %);

${sin\left( x\right) }^{4}-3\,{sin\left( x\right) }^{2}+cos\left( x\right) \,\left( 2-{sin\left( x\right) }^{2}\right) +3\leqno{(\%o3) }$

2.8.1 Нахождение корней уравнений и систем алгебраических уравнений

Решение алгебраических уравнений и их систем осуществляется при помощи функции solve , в качестве параметров. В первых квадратных скобках указывается список уравнений через запятую, во вторых — список переменных, через запятую (либо несколько упрощённые формы записи):

— решение одного уравнения относительно переменной ;
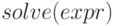— решение уравнения с одной неизвестной и числовыми коэффициентами;
— решение системы уравнений.

Примеры:

Решение одного уравнения с одним неизвестным

(%i7)	solve(x^2-5*x+4);

$[x=1,x=4]\leqno{(\%o7) }$

Решение одного уравнения в символьном виде:

(%i2)	solve([x-a/x+b], [x]);

$[x=-\frac{\sqrt{{b}^{2}+4\,a}+b}{2},x=\frac{\sqrt{{b}^{2}+4\,a}-b}{2}]\leqno{(\%o2) }$

Решение системы уравнений в символьном виде:

(%i10)	solve([x*y/(x+y)=a,x*z/(x+z)=b,y*z/(y+z)=c], [x,y,z]);

$\begin{math} (\%o10) [[x=0,y=0,z=0], [x=\frac{2abc}{\left( b+a\right) c-ab}, y=\frac{2abc}{\left( b-a\right) c+ab}, z=-\frac{2abc}{\left( b-a\right) c-ab}]] \end{math}$

В последнем примере решений несколько, и Maxima выдаёт результат в виде списка.

Функция solve применима и для решения тригонометрических уравнений. При этом в случае множества решений у тригонометрических уравнений выдаётся соответствующее сообщение только и одно из решений.

Пример:

(%i13) solve([sin(x)=0], [x]);

solve: using arc-trig functions to get a solution.
Some solutions will be lost.

$[x=0]\leqno{(\%o13) }$

Также Maxima позволяет находить комплексные корни

(%i18)	solve([x^2+x+1], [x]);

$[x=-\frac{\sqrt{3}\,i+1}{2},x=\frac{\sqrt{3}\,i-1}{2}]\leqno{(\%o18) }$